Непрерывное вейвлет-преобразование в анализе бизнес-информации
Анализ бизнес-информации является необходимым условием при планировании деятельности предприятия, принятии решений, поиске путей повышения прибыльности. Грамотный анализ бизнес-данных и правильное использование полученной информации позволяет значительно повысить эффективность работы предприятия. При этом, учитывая высокую динамичность современного бизнеса, зачастую возникает необходимость быстрого и, как следствие, почти интуитивного принятия решения по тому или иному вопросу.
В этих условия огромную роль приобретает наглядность представления аналитической информации – не секрет, что графическую информацию (схемы, графики, карты) человек воспринимает лучше, чем сухой язык цифр. Анализ данных с использованием непрерывного вейвлет-преобразования является удобным, надежным и мощным инструментом исследования бизнес-процессов и позволяет представить результаты в очень наглядном виде, удобном для изучения и интерпретации.
Аналитические показатели бизнес-информации: периодичность, тренд, локальные особенности
Одним из важнейших аналитических показателей бизнес-процесса является его периодичность, т.е. повторяемость через определенные промежутки времени. Пример – сезонные колебания загородных перевозок (очевидно, что летом люди ездят за город чаще, чем зимой) или недельные колебания розничных продаж (в выходные люди уделяют больше времени покупкам, чем в будние дни).
Наличие информации о периодических составляющих бизнес-процесса и глубине их колебаний позволяет грамотно планировать деятельность предприятия на основании данных предыдущих периодов, а также эффективно распределять резервы в течение периода, в зависимости от его фазы (спад, подъем, текущий пик или упадок).
Однако, комбинация нескольких различных колебаний может иметь настолько сложную форму, что выявить их наличие "на взгляд" не представляется возможным.
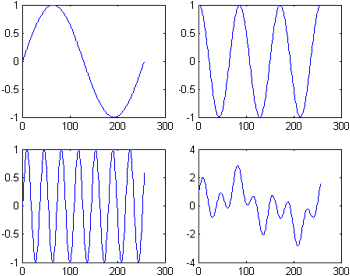
Другим важным показателем является тренд, т.е. выраженная тенденция движения бизнеса (постоянный спад или подъем). Тренд показывает динамику развития бизнеса вне зависимости от периодических колебаний. Очевидно, что возрастающий тренд позитивных факторов (прибыли), либо убывающий тренд негативных (расходов), является показателем успешной деятельности предприятия.
Как и в предыдущем случае, наличие тренда может быть неочевидным при простом рассмотрении бизнес-данных – например, если незначительный тренд "замаскирован" сильными колебаниями.
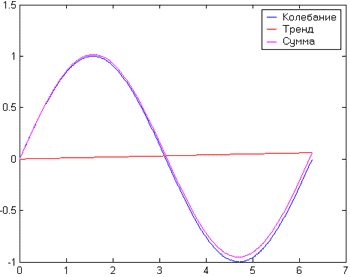
Еще одним важным фактором, который необходимо учитывать при анализе бизнес-информации, являются локальные особенности, т.е. резкие, скачкообразные изменения характеристик бизнес-процесса.
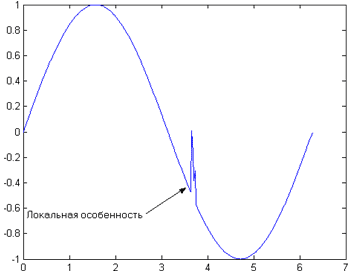
Локальные особенности могут иметь как случайный (например, падение производства в результате форс-мажорных обстоятельств у поставщиков), так и систематический характер (резкий рост продаж в предпразничные дни с таким же скачкообразным возвратом к предыдущему уровню после праздников).
Другим примером может служить скачкообразный рост продаж после удачной рекламной кампании. Конечно, от случайностей не застрахован никто, но знание закономерности систематических особенностей позволит не только избежать связанных с ними проблем, но даже извлечь из них выгоду.
Например, валютные спекулянты получают наибольшую прибыль именно в момент скачкообразных изменений рынка (разумеется, в том случае, если они знают или догадываются о предстоящем скачке и грамотно играют на этой информации). С другой стороны, локальные особенности искажают реальную картину бизнеса и могут "маскировать" другие важные факторы – такие, как периодические зависимости или краткосрочный тренд.
Грамотный анализ локальных особенностей позволяет, во-первых, восстановить информацию о течении бизнес-процесса в "спокойных", стабильных условиях и получить более достоверную аналитическую информацию, и, во-вторых, быть готовым к подобным ситуациям в дальнейшем и пройти через них с наименьшими потерями.
Сущность непрерывного вейвлет-преобразования
Любая закономерность, описывающая некоторый бизнес-процесс, ограничена как во времени (любой бизнес-процесс имеет начало и конец), так и по величине. Из курса математического анализа известно, что такая закономерность может быть представлена в виде суммы гармонических колебаний различной частоты и интенсивности (амплитуды).
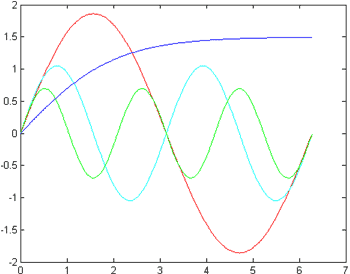
При этом колебания, имеющие низкую частоту, отвечают за медленные, плавные, крупномасштабные изменения описываемой величины, а высокочастотные – за короткие, мелкомасштабные изменения. Чем сильнее изменяется описываемая данной закономерностью величина на данном масштабе, тем большую амплитуду имеют составляющие на соответствующей частоте.
Таким образом, любой бизнес-процесс можно рассматривать как во временной области (т.е. развитие процесса во времени), так и в частотной области (т.е. в плане масштаба изменений исследуемой величины). Говорят также о поведении процесса в частотно-временной области – т.е. о закономерности, описывающей процесс в зависимости как от времени, так и от частоты (масштаба изменений).
Вейвлетом называется некоторая функция (закономерность), хорошо локализованная (т.е. сосредоточенная в небольшой окрестности некоторой точки и резко убывающая до нуля по мере удаления от нее) как во временной, так и в частотной области.
Отметим, что вейвлет – это не какая-то конкретная математическая зависимость или "формула", а любой объект или процесс, обладающий указанными особенностями (и еще некоторыми математическими свойствами, рассмотрение которых выходит за рамки этой статьи). Существуют вейвлеты, имеющие самые различные свойства и подходящие для решения самых разных задач.
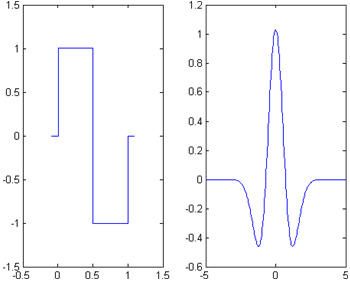
К вейвлету можно применить две операции:
- сдвиг, т.е. перемещение области его локализации во времени;
- масштабирование (растяжение или сжатие), т.е. перемещение области его локализации по частоте.
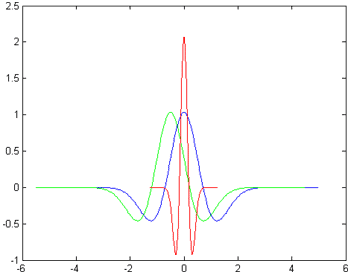
Использование этих операций, с учетом свойства локальности вейвлета в частотно-временной области, позволяет анализировать данные на различных масштабах и точно определять положение их характерных особенностей во времени.
Идея непрерывного вейвлет-преобразования заключается в вычислении скалярного произведения (величины, показывающей степень "похожести" двух закономерностей) исследуемых данных с различными сдвигами некоторого вейвлета на разных масштабах. В результате получается набор коэффициентов, показывающих, насколько поведение процесса в данной точке похоже на "поведение" вейвлета на данном масштабе.
Чем ближе вид анализируемой зависимости в окрестности данной точки к виду вейвлета, тем большую абсолютную величину имеет соответствующий коэффициент. Отрицательные коэффициенты показывают, что зависимость похожа на "зеркальное отражение" вейвлета.
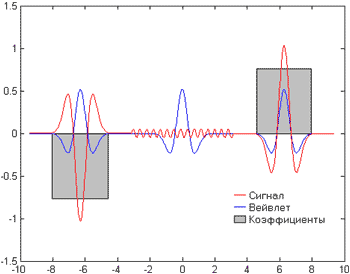
Полученные коэффициенты можно представить в графическом виде, если по одной оси отложить сдвиги вейвлета (ось времени), а по другой – масштабы (ось масштабов), и "раскрасить" точки получившейся схемы в зависимости от величины соответствующих коэффициентов: чем больше значение коэффициента, тем ярче цвет. Получившееся изображение называют картой коэффициентов преобразования, или просто картой преобразования.
Карта преобразования – это как бы "рентгеновский снимок" исследуемого процесса. На ней видны все его характерные особенности: масштаб и интенсивность периодических изменений, направление и величина трендов, наличие, расположение и длительность скачков – то есть все факторы, предложенные нами выше для анализа бизнес-информации.
Интерпретация карты преобразования
Покажем, как проанализировать полученную карту преобразования и выделить из нее полезные сведения о характеристиках бизнес-процесса.
Во-первых, полезно проанализировать энергию коэффициентов преобразования на каждом мастштабе. Энергия равна сумме квадратов значений коэффициентов, поэтому те масштабы, на которых большее количество коэффициенты имеют большое абсолютное значение, будут соответствовать более высоким значениям энергии.
Такие масштабы несут наибольшее количество информации об исследуемом процессе, и должны быть изучены более внимательно. С другой стороны, масштабы, обладающие низкими значениям энергии, практически не содержат полезной информации и могут быть исключены из рассмотрения.
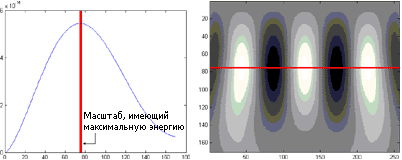
Как уже говорилось выше, периодические изменения (колебания), происходящие с определенной частотой, однозначно соответствуют некоторому масштабу изменений. Поскольку вейвлеты имеют хорошую локализацию по частоте, то на карте преобразования эти колебания выглядят как цепочка "холмов", имеющих "вершины" на масштабе, соответствующем частоте колебаний и расположенные в точках (по оси времени), в которых эти изменения достигают наибольших значений (соответственно, "дно" впадин между холмами приходится на точки наименьшего значения колебаний).
Если в течение всего исследуемого процесса изменения происходят с одной и той же частотой, то "холмы" располагаются на одной линии вдоль оси времени, и расстояние между их вершинами всегда одно и то же (и равно периоду колебаний). Если же частота колебаний изменяется, то вершины "сдвигаются" в направлении соответствующего изменения масштаба, и расстояние между ними тоже изменяется.
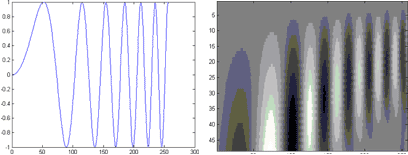
Тренд отражается на карте преобразования как плавное изменение яркости вдоль оси времени одновременно (но с разной интенсивностью) на всех масштабах. Если тренд нарастающий, то яркость будет увеличиваться, если убывающий – уменьшаться. Наличие нескольких последовательных трендов представляется в виде поочередного нарастания и убывания яркости точек на карте, при этом точка изменения тренда имеет наибольшую или наименьшую яркость.
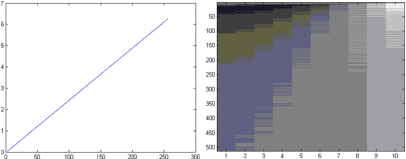
Локальные особенности представлены на карте преобразования как линии резкого перепада яркости, исходящие из точки, соответствующей времени возникновения скачка. Если эти точки расположены на одинаковом расстоянии друг от друга (т.е. налицо периодичность процесса), то можно говорить о систематическом характере выбросов.
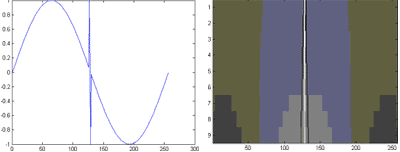
Таким образом, каждый фактор бизнес-процесса имеет свой, характерный отпечаток на карте коэффициентов преобразования, а его величина выражается яркостью соответствующего отпечатка, и вся аналитическая информация представляется в наглядном и удобном для изучения виде.
Характеристики бизнес-процессов имеют, как правило, сильно отличающуюся интенсивность. Поэтому некоторые (протяженные во времени и небольшие по значению) изменения могут быть незаметны на фоне ярко выраженных, интенсивных явлений.
Чтобы извлечь из результатов исследования как можно больше полезной информации, желательно выполнять анализ в несколько этапов, постепенно выявляя как наиболее явные, так и наименее значимые факторы и уничтожая их влияние на исследуемые данные. Однако, благодаря наглядности представления результатов в виде карты преобразования, иногда достаточно беглого взгляда, чтобы увидеть на ней наиболее яркие факторы и быстро принять правильное решение.