Основы теории вейвлет-преобразования

Предобработка данных22 комментарияВерсия для печати

Введение

Некоторые идеи теории вейвлетов появились очень давно. Например, уже в 1910 году А.Хаар опубликовал полную ортонормальную систему базисных функций с локальной областью определения (теперь они называются вейвлетами Хаара). Первое упоминание о вейвлетах появилось в литературе по цифровой обработке и анализу сейсмических сигналов (работы А.Гроссмана и Ж.Морле).

В последнее время возникло и оформилось целое научное направление, связанное с вейвлет-анализом и теорией вейвлет-преобразования. Вейвлеты широко применяются для фильтрации и предварительной обработки данных, анализа состояния и прогнозирования ситуации на фондовых рынках, распознавания образов, при обработке и синтезе различных сигналов, например речевых, медицинских, для решения задач сжатия и обработки изображений, при обучении нейросетей и во многих других случаях.

Несмотря на то, что теория вейвлет-преобразования уже в основном разработана, точного определения, что же такое "вейвлет", какие функции можно назвать вейвлетами, насколько мне известно, не существует. Вейвлеты могут быть ортогональными, полуортогональными, биортогональными. Эти функции могут быть симметричными, асимметричными и несимметричными.

Различают вейвлеты с компактной областью определения и не имеющие таковой. Некоторые функции имеют аналитическое выражение, другие – быстрый алгоритм вычисления связанного с ними вейвлет-преобразования. Попробуем дать вначале неформальное определение вейвлет-преобразования, а затем – его точное математическое обоснование.

Вейвлеты и многомасштабный анализ

Рассмотрим задачу, которая очень часто встречается на практике: у нас есть сигнал (а сигналом может быть все, что угодно, начиная от записи показаний датчика и кончая оцифрованной речью или изображением). Идея многомасштабного анализа (multiscale analysis, multiresolutional analysis) заключается в том, чтобы взглянуть на сигнал сначала вплотную – под микроскопом, затем через лупу, потом отойти на пару шагов, потом посмотреть издалека (рис.1).

Что это нам дает? Во-первых, мы можем, путем последовательного огрубления (или уточнения) сигнала выявлять его локальные особенности (ударение в речи или характерные детали изображения) и подразделять их по интенсивности. Во-вторых, таким образом обнаруживается динамика изменения сигнала в зависимости от масштаба.

Если резкие скачки (например, аварийное отклонение показаний датчика) во многих случаях видны "невооруженным глазом", то взаимодействия событий на мелких масштабах, перерастающие в крупномасштабные явления (так, мощный транспортный поток состоит из движения многих отдельных автомобилей), увидеть очень сложно. И наоборот, сосредоточившись только на мелких деталях, можно не заметить явлений, происходящих на глобальном уровне.

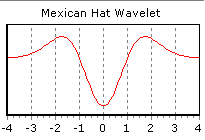
Идея применения вейвлетов для многомасштабного анализа заключается в том, что разложение сигнала производится по базису, образованному сдвигами и разномасштабными копиями функции-прототипа (то есть вейвлет-преобразование по своей сути является фрактальным). Такие базисные функции называются вейвлетами (wavelet), если они определены на пространстве L²(R) (пространство комплекснозначных функций f(t) на прямой с ограниченной энергией), колеблются вокруг оси абсцисс и быстро сходятся к нулю по мере увеличения абсолютного значения аргумента (рис.2).

Оговоримся сразу, что это определение не претендует на полноту и точность, а дает лишь некий "словесный портрет" вейвлета. Таким образом, свертка сигнала с одним из вейвлетов позволяет выделить характерные особенности сигнала в области локализации этого вейвлета, причем чем больший масштаб имеет вейвлет, тем более широкая область сигнала будет оказывать влияние на результат свертки.

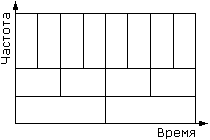
Согласно принципу неопределенности, чем лучше функция сконцентрирована во времени, тем больше она размазана в частотной области. При перемасштабировании функции произведение временного и частотного диапазонов остается постоянным и представляет собой площадь ячейки в частотно-временной (фазовой) плоскости.

Преимущество вейвлет-преобразования перед, например, преобразованием Габора заключается в том, что оно покрывает фазовую плоскость ячейками одинаковой площади, но разной формы (рис.3). Это позволяет хорошо локализовать низкочастотные детали сигнала в частотной области (преобладающие гармоники), а высокочастотные – во временной (резкие скачки, пики и т.п.).

Более того, вейвлет-анализ позволяет исследовать поведение фрактальных функций – то есть не имеющих производных ни в одной своей точке!

Ортогональное вейвлет-преобразование

Вейвлет-преобразование несет огромное количество информации о сигнале, но, с другой стороны, обладает сильной избыточностью, так как каждая точка фазовой плоскости оказывает влияние на его результат.

Вообще говоря, для точного восстановления сигнала достаточно знать его вейвлет-преобразование на некоторой довольно редкой решетке в фазовой плоскости (например, только в центре каждой ячейки на рис.3). Следовательно, и вся информация о сигнале содержится в этом довольно небольшом наборе значений.

Идея здесь заключается в том, чтобы масштабировать вейвлет в некоторое постоянное (например, 2) число раз, и смещать его во времени на фиксированное расстояние, зависящее от масштаба. При этом все сдвиги одного масштаба должны быть попарно ортогональны – такие вейвлеты называются ортогональными.

При таком преобразовании выполняется свертка сигнала с некоторой функцией (так называемой скейлинг-функцией, о ее свойствах мы расскажем позже) и с вейвлетом, связанным с этой скейлинг-функцией. В результате мы получаем "сглаженную" версию исходного сигнала и набор "деталей", отличающих сглаженный сигнал от исходного.

Последовательно применяя такое преобразование, мы можем получить результат нужной нам степени детальности (гладкости) и набор деталей на разных масштабах – то, о чем говорили в начале статьи. Более того, применив вейвлет-преобразование к заинтересовавшей нас детали сигнала, мы можем получить ее "увеличенное изображение". И наоборот, отбросив несущественные детали и выполнив обратное преобразование, мы получим сигнал, очищенный от шумов и случайных выбросов (например, "убрать" случайно попавшую в кадр птицу на фотографии здания).

Дискретное вейвлет-преобразование и другие направления вейвлет-анализа

Очевидно, идея использовать вейвлет-преобразование для обработки дискретных данных является весьма привлекательной (дискретизация данных необходима, например, при их обработке на ЭВМ). Основная трудность заключается в том, что формулы для дискретного вейвлет-преобразования нельзя получить просто дискретизацией соответствующих формул непрерывного преобразования.

К счастью, И.Добеши удалось найти метод, позволяющий построить (бесконечную) серию ортогональных вейвлетов, каждый из которых определяется конечным числом коэффициентов. Стало возможным построить алгоритм, реализующий быстрое вейвлет-преобразование на дискретных данных (алгоритм Малла). Достоинство этого алгоритма, помимо всего вышесказанного, заключается в его простоте и высокой скорости: и на разложение, и на восстановление требуется порядка cN операций, где с – число коэффициентов, а N – длина выборки.

В последнее время теория вейвлет-преобразования переживает просто революционный рост. Появились и развиваются такие направления, как биортогональные вейвлеты, мультивейвлеты, вейвлет-пакеты, лифтинг и т.д.

Применение вейвлет-преобразования

В заключение нашей статьи перечислим некоторые области, где использование вейвлетов может оказаться (или уже является) весьма перспективным.

1. Обработка экспериментальных данных. Поскольку вейвлеты появились именно как механизм обработки экспериментальных данных, их применение для решения подобных задач представляется весьма привлекательным до сих пор. Вейвлет-преобразование дает наиболее наглядную и информативную картину результатов эксперимента, позволяет очистить исходные данные от шумов и случайных искажений, и даже "на глаз" подметить некоторые особенности данных и направление их дальнейшей обработки и анализа. Кроме того, вейвлеты хорошо подходят для анализа нестационарных сигналов, возникающих в медицине, анализе фондовых рынков и других областях.
2. Обработка изображений. Наше зрение устроено так, что мы сосредотачиваем свое внимание на существенных деталях изображения, отсекая ненужное. Используя вейвлет-преобразование, мы можем сгладить или выделить некоторые детали изображения, увеличить или уменьшить его, выделить важные детали и даже повысить его качество!
3. Сжатие данных. Особенностью ортогонального многомасштабного анализа является то, что для достаточно гладких данных полученные в результате преобразования детали в основном близки по величине к нулю и, следовательно, очень хорошо сжимаются обычными статистическими методами. Огромным достоинством вейвлет-преобразования является то, что оно не вносит дополнительной избыточности в исходные данные, и сигнал может быть полностью восстановлен с использованием тех же самых фильтров. Кроме того, отделение в результате преобразования деталей от основного сигнала позволяет очень просто реализовать сжатие с потерями – достаточно просто отбросить детали на тех масштабах, где они несущественны! Достаточно сказать, что изображение, обработанное вейвлетами, можно сжать в 3-10 раз без существенных потерь информации (а с допустимыми потерями – до 300 раз!). В качестве примера отметим, что вейвлет-преобразование положено в основу стандарта сжатия данных MPEG4.
4. Нейросети и другие механизмы анализа данных. Большие трудности при обучении нейросетей (или настройке других механизмов анализа данных) создает сильная зашумленность данных или наличие большого числа "особых случаев" (случайные выбросы, пропуски, нелинейные искажения и т.п.). Такие помехи способны скрывать характерные особенности данных или выдавать себя за них и могут сильно ухудшить результаты обучения. Поэтому рекомендуется очистить данные, прежде чем анализировать их. По уже приведенным выше соображениям, а также благодаря наличию быстрых и эффективных алгоритмов реализации, вейвлеты представляются весьма удобным и перспективным механизмом очистки и предварительной обработки данных для использования их в статистических и бизнес-приложениях, системах искусственного интеллекта и т.п.
5. Системы передачи данных и цифровой обработки сигналов. Благодаря высокой эффективности алгоритмов и устойчивости к воздействию помех, вейвлет-преобразование является мощным инструментом в тех областях, где традиционно использовались другие методы анализа данных, например, преобразование Фурье. Возможность применения уже существующих методов обработки результатов преобразования, а также характерные особенности поведения вейвлет-преобразования в частотно-временной области позволяют существенно расширить и дополнить возможности подобных систем.

И это еще далеко не все!

Заключение

Несмотря на то, что математический аппарат вейвлет-анализа хорошо разработан и теория, в общем, оформилась, вейвлеты оставляют обширное поле для исследований. Достаточно сказать, что выбор вейвлета, наиболее подходящего для анализа конкретных данных, представляет собой скорее искусство, чем рутинную процедуру. Кроме того, огромное значение имеет задача разработки приложений, использующих вейвлет-анализ – как в перечисленных областях, так и во многих других, перечислить которые просто не представляется возможным.