Очистка персональных данных, часть 2
Проблема очистки персональных данных от ошибок уже затрагивалась в предыдущей статье.
В данной статье пойдет речь о выявлении и устранении ошибок при помощи методов, основанных на понятиях математической статистики. Для этого рассчитываются определенные показатели. Вычисления производятся по всем имеющимся данным, охватывая весь диапазон значений, принимаемых признаками.
На основе полученных результатов одни методы могут выделить подозрительную информацию, которая сильно отличается от остальных, а другие – вычислить величины, которые предположительно более всего похожи на истинные.
Таким образом, анализируя сведения с помощью статистических характеристик, можно оценить общую картину данных и на ее фоне определить возможные ошибки с последующим их исправлением на подобранные похожие значения.
Различают несколько типов данных. Каждый из них обрабатывается по-своему. Рассмотрим основные типы данных.
Типы данных
Персональные данные по своей природе разнородны. Их условно можно разбить на следующие типы:
- Качественные данные. Они представляют собой некоторые свойства объектов, которые нельзя количественно измерить (например, название профессии, национальность).
- Категориальные данные. К ним относятся качественные данные, принимающие значения из некоторого ограниченного набора категорий.
Для примера возьмем поле "Семейное положение". Список вводимых в него значений ограничен и состоит из следующих категорий: "замужем/женат", "не замужем/не женат", "вдова/вдовец", "разведена/разведен" или "гражданский брак".
Со значениями категориальных данных непосредственно невозможно производить статистические операции, так как они относятся к нечисловому типу данных. Для решения этой проблемы используют такую характеристику, как частота появления каждой категории во всей имеющейся информации. Она описывает данные количественно и позволяет сравнивать их между собой, находить взаимосвязи и производить другие операции.
- Ординальные данные. Они отличаются от категориальных данных тем, что все категории ординальных данных упорядочены.
Например, значения, которые можно ввести в поле "Образование", делятся на следующие категории: "начальное", "среднее", "среднее специальное", "незаконченное высшее", "высшее". По смыслу каждое из них можно сравнить друг с другом при помощи знака неравенства "<", то есть "начальное" < "среднее" < "среднее специальное" < "незаконченное высшее" < "высшее".
Ординальные данные обрабатываются так же, как и категориальные. Кроме того, их можно закодировать, поставив каждой категории соответствующее число (ранг), который сохранил бы существующий порядок (например, для категории "начальное" ранг равен "1"). Преобразованные значения уже не относятся к строковому типу и могут участвовать в статистическом анализе.
- Количественные данные. Они представляют собой некоторые свойства объектов, которые принимают числовые значения.
Количественную информацию при анализе можно распределить по шкале, разбив ее на равные интервалы (например, рост человека укладывается в следующие диапазоны: от 150 до 160, от 160 до 170 и т.д.).
Одной из главных характеристик поведения числовых данных, от которой зависит процесс очистки информации, является закон распределения. Он описывает соответствие между возможными значениями случайной величины и вероятностями их появления.
- Дискретные данные. К ним относятся данные, которые принимают отдельные значения из возможного набора чисел. Для таких величин характерно то, что их общее количество может быть подсчитано при помощи натуральных чисел от одного до бесконечности.
Число детей в семье; количество клиентов, купивших автомобиль за определенный период, – всё это дискретные данные. Они принимают определенные целочисленные значения.
- Непрерывные данные. К ним относятся числовые данные, принимающие любые числовые значения из некоторого интервала.
К непрерывным персональным данным относятся: вес человека (например, у взрослого он может принимать значения от 50 до 150 кг), рост, средний доход и т.д.
Учитывая различия в типах персональных данных, применяют несколько статистических методов очистки информации. Каждый из них по-своему обнаруживает вероятные ошибки в сведениях и подбирает допустимые значения для их замены.
Методы очистки данных
Вычисление частот появления значений
Данный метод основывается на анализе частоты появления определенного значения во всей совокупности данных. Для этого сначала подсчитывается, какое количество раз различные значения были введены. Далее они сортируются в порядке убывания их частот. Таким образом, в конце списка оказываются значения, которые реже всего вводились респондентами.
Вполне возможно, что в них были допущены опечатки, оставлены пустые поля, введены аномальные значения. Эти поля подвергаются дополнительной обработке и последующей замене, если такое решение примет эксперт, с помощью методов, описанных в предыдущей статье.
Данный метод подходит для очистки как качественных данных, так и дискретных значений.
Рассмотрим различные способы написания женского имени "Ольга", которые могли быть введены респондентами при заполнении анкет (таблица 1). Проанализируем частоту появления каждого значения среди ста анкет, а также вычислим расстояние Левенштейна между редко введенными значениями и словами из словаря женских имен для очистки "загрязненной" информации (способы вычисления степени близости значений приведены в предыдущей статье).
Таблица 1 – Различные способы ввода имени "Ольга"
| Имя | Частота появления | Расстояние Левенштейна до имени "Ольга" |
|---|---|---|
| Ольга | 84 |
0 |
| Оля | 10 |
4 |
| Олгьа | 2 |
2 |
| Олга | 2 |
1 |
| Ольг а | 1 |
1 |
| Ольгав | 1 |
1 |
Из содержания таблицы следует, что чем меньше частота появления слова в анкете, тем вероятней, что в нем допущена ошибка.
Для нашего примера зададим допустимый порог обнаружения ошибок, равный двум. Те значения, у которых расстояние Левенштейна меньше величины заданного порога, можно заменить похожим именем из женского словаря. На основании этого утверждения имена "Олга", "Олгьа", "Ольг а" и "Ольгав" заменяются именем "Ольга".
Таким образом, с помощью метода вычисления частот удалось обнаружить данные с возможными опечатками, а с помощью метода анализа строк - восстановить их вероятные значения.
Метод вычисления частот также может обнаруживать ошибки при исследовании совместной частоты появления двух признаков объектов. Для этого составляется таблица сопряженности. По строкам в ней находятся значения одной характеристики данных, а по столбцам – другой. На их пересечении указывается частота, с которой они совместно появляются во всей совокупности данных. В зависимости от величины частоты можно определить существует ли вероятность "загрязнения" данных или нет.
Пример
С помощью таблицы сопряженности можно выявлять и устранять противоречия в полях анкеты.
Часто возникают несоответствия между вводимым именем респондента и его полом. Составим таблицу, в которой по столбцу будут отображаться имена, по строке – пол, а на их пересечении – количество человек, которые указали соответствующему имени данный пол (таблица 2).
Таблица 2 – Взаимосвязь между именем респондента и указанным в анкете полом
| Имя | Женский пол | Мужской пол |
|---|---|---|
| Александр | 20 |
80 |
| Андрей | 2 |
98 |
| Елена | 99 |
1 |
| Дмитрий | 3 |
97 |
| Юлия | 99 |
1 |
Между полом и полными русскими именами за редким исключением существует взаимно однозначное соответствие. Если при изучении таблицы сопряженности в строке преобладает значение одного из столбцов, то, скорее всего, в других содержится ошибка. Например, двадцать респондентов с именем "Александр", возможно, сделали опечатку при указании своих персональных данных. Нужно еще раз просмотреть анкеты этих людей, и если больше не будет никаких противоречий, то поменять значение "Женский" на "Мужской".
Метод вычисления частот используется для устранения различных видов ошибок, таких как пропуски, аномалии, опечатки, неправдоподобие данных. Он рассчитан для анализа часто встречающихся слов. Редко употребляемое правильно записанное слово может быть принято за ошибку. В данной ситуации нужно оценить вероятность наступления такого события.
Если разница между частотой появления проверяемой переменной и частотой появления большинства других значений велика и многие значения отличаются друг от друга, то вероятнее всего, что значение введено правильно. Однако этого недостаточно для автоматической замены подозрительного значения на подобранное слово. Необходимо провести дополнительный анализ с использованием других методов и предоставить все полученные результаты эксперту. Уже он будет определять наличие ошибки в оцениваемых данных, а также принимать решение о замене "загрязненной" информации на подобранные значения.
Вычисление средних значений
Среднее значение – обобщающая характеристика изучаемого признака в совокупности данных.
Используется несколько видов средних значений:
- Среднее арифметическое значение. Рассчитывается как частное от деления суммы значений признака на их количество.
- Медиана. Определяется как центральное значение упорядоченной совокупности данных, которое делит эти данные на равные половины. Одна половина значений будет располагаться выше медианы, а другая – ниже.
- Мода. Представляет собой значение, которое чаще всего встречается в исследуемой совокупности. Это единственная характеристика, которая может быть вычислена для категориальных данных.
Пример
При заполнении резюме на сайте Сидорова С. С. не ввела данные в графу "Ожидаемая зарплата". Работодатель при подборе сотрудников задал определенное значение для поля "Зарплата". Таким образом, в результатах его поиска анкета Сидоровой С. С. не отобразилась, даже при том, что данные удовлетворяли всем остальным критериям поиска. Системы, используемые в кадровых агентствах, должны учитывать подобного рода пропуски в анкетах и уметь заполнять их наиболее подходящими значениями.
Выделим всех соискателей, у которых в резюме указаны такие же данные: год рождения, город, наименование учебного заведения и должность, что и у Сидоровой С. С. После этого вычислим предполагаемое пропущенное значение для поля "Ожидаемая зарплата", рассчитав все виды средних значений (таблица 3).
Таблица 3 – Данные для вычисления средних значений
| ФИО | Ожидаемая зарплата, руб. |
|---|---|
| Алексеев А. А. | 20000 |
| Алешина А. А. | 18000 |
| Иванов И. И. | 25000 |
| Петров П. П. | 20000 |
| Федорова Ф. Ф. | 21000 |
- Среднее арифметическое значение
Рассчитаем статистическую характеристику:
$$\bar{x}=\frac{(20000 + 18000 + 25000 + 20000 + 21000)}{5}=20800$$
- Медиана
Расположим все встречающиеся значения в порядке возрастания и найдем медиану:
18000 20000 20000 21000 25000
Медиана принимает значение, равное 20000 руб.
- Мода
Подсчитаем частоту появления каждого из значений (таблица 4).
Таблица 4 – Определение моды
Значение 18000200002100025000Частота появления 1211Из таблицы 4 следует, что мода равняется 20000 руб., так как это наиболее часто встречающееся значение.
Все средние значения получились приблизительно одинаковыми. Таким образом, пропущенное поле может быть заполнено любой из вышеприведенных характеристик. Теперь при поиске сотрудников система будет выдавать анкеты всех потенциальных кандидатов путем предсказания недостающих данных с помощью метода средних значений.
Если данные содержат большой разброс значений, то метод средних применяется не к отдельному объекту, а к целой группе. Все данные в этом случае разбиваются на группы, содержащие приблизительно однородные элементы с похожими признаками. Внутри каждой из них рассчитывается средняя величина, которая будет типична именно для тех объектов, которые входят в эту группу. Анализируя данные таким методом, можно отыскать скрытые ошибки, незаметные при обработке всей совокупности данных.
Пример
Рассмотрим и проверим данные о трудовом стаже, которые указали мужчины-респонденты при заполнении анкет (таблица 5).
Таблица 5 – Данные для определения групповых средних значений
| ФИО | Возраст | Стаж |
|---|---|---|
| Ильин И. И. | 19 |
2 |
| Железов А. А | 20 |
1 |
| Зубин З. З. | 20 |
5 |
| Игнатов И. И. | 20 |
5 |
| Колин В. В. | 20 |
5 |
| Николаев Л. Л. | 20 |
45 |
| Манов М. М. | 21 |
6 |
| ... | ... |
... |
| Чудов С. С. | 70 |
45 |
Если анализировать только колонку "Стаж", то существенных ошибок в приведенных цифрах можно не заметить. Для того чтобы выявить отклонения, в таблице приведены данные о возрасте людей, заполнивших анкеты. С их помощью всех респондентов можно разделить на соответствующие возрастные категории (группы "19 лет", "20 лет" и т.д.). В этом случае данные анализируются в каждой группе и те величины, которые сильно отличаются от остальных, проверяются на наличие ошибок и могут заменяться средними групповыми значениями.
Стаж, указанный респондентом Николаевым Л.Л., для его категории слишком большой. При дополнительной проверке было подтверждено наличие опечатки в исследуемом значении, так как трудовой стаж превышает возраст респондента. Допущенную ошибку можно заменить, например, средней арифметической величиной, рассчитанной по данным о стаже людей его возраста. Вычисленное групповое значение получается равным 4. Им заменяется стаж респондента Николаева, и так происходит очистка полей от аномалий.
Метод вычисления средних значений используется при заполнении пропусков в данных, так как эта статистическая характеристика оценивает в целом всю информацию. Применение средней арифметической величины уместно в том случае, когда значения имеют нормальный закон распределения. Медиана менее чувствительна к выбросам, поэтому ее предпочтительней использовать при наличии аномальных величин. Мода применяется, когда данные не подчиняются нормальному закону распределения, так как она характеризует наиболее популярное значение признака.
Метод средних значений довольно прост в реализации, но его применение может не только восстановить картину исходных данных, а, наоборот, ее исказить. Это связано с тем, что многие величины так различаются между собой, что среднее значение не дает в целом представления об имеющейся совокупности элементов.
Учитывая данное обстоятельство, следует с осторожностью подходить к процессу очистки информации с помощью метода средних значений. Прежде чем исправлять "загрязненные" данные, нужно сначала тщательно их оценить (учитывать степень разброса, количество неповторяющихся значений, объем информации и т.д.), а затем решить, воспользоваться ли для замены наиболее подходящей средней величиной или нет.
Интервальный метод
С помощью данного метода вычисляется интервал, называемый доверительным, между границами которого с заданной вероятностью находятся истинные значения оцениваемых параметров (то есть если доверительная вероятность равна 95%, то с вероятностью 95% можно сказать, что все истинные значения совокупности данных лежат в указанном интервале).
Доверительный интервал с вероятностью 95% для большого объема данных, подчиняющихся нормальному закону распределения, определяется по формуле:
$\bar{x} - \frac{1.96 \times \sigma }{\sqrt{n}}< x_i< \bar{x} +\frac{1.96 \times \sigma }{\sqrt{n}}$,
где
$x_i$ – исследуемый ряд данных,
$y_i$ – ранги значений, принимаемых признаком $Y$,
$\sigma$ – среднеквадратическое отклонение,
$n$ – количество исследуемых данных.
Среднеквадратическое отклонение вычисляется по формуле:
$$\sigma = \sqrt{\frac{\sum \limits_{1}^{n}(x_t - \bar{x})^2}{n-1}}$$
Те значения, которые не попали в доверительный интервал, являются потенциальными ошибками. Эксперт в таком случае может принять решение о возможной замене их подобранными значениями (например, средней арифметической величиной).
Интервальный метод в основном применяется для однородных данных. Чтобы определить степень однородности исследуемой информации, используют коэффициент вариации, вычисляемый по формуле:
$$V_{\sigma} = \frac{\sigma }{\bar {x}} \times 100\%$$
.Если коэффициент вариации больше 33,3%, то считается, что степень разброса значений велика. В этом случае данный метод, скорее всего, не подходит для поиска ошибок, так как доверительный интервал будет включать слишком большой диапазон значений. Чтобы решить эту проблему, можно сгруппировать похожие данные, и для каждой группы рассчитать свой доверительный интервал.
Пример
Отыщем в данных о возрасте студентов аномальные значения, возникшие в результате опечаток операторов при наборе текста (таблица 6). Для этого вычислим доверительный интервал для имеющихся данных.
Таблица 6 – Данные о возрасте студентов
| ФИО | Возраст |
|---|---|
| Иванов И. И. | 18 |
| Петров П. П. | 19 |
| Алексеев А. А. | 9 |
| Сидорова С. С. | 20 |
| Алешина А. А. | 21 |
| Федорова Ф. Ф. | 20 |
Подставив требуемые величины в вышеприведенную формулу, доверительный интервал получается равным (14; 22), а коэффициент вариации – 25%. Из этого следует, что с помощью интервального метода можно выявить ошибки в данном случае.
В доверительный интервал не вошел возраст студента Алексеева А. А., что говорит о возможной опечатке в его записи. С помощью различных методов эксперт подбирает вероятные значения этой сомнительной величине. В данном случае такими значениями могут быть "19" (при записи возраста могла быть пропущена "1"), "20" (чаще всего вводимый возраст) и т.п. Эксперт, исходя из ситуации, может заменить число "9" любой из этих величин.
Данный метод позволяет выявлять в количественной информации аномальные величины. Они сильно отличаются от присутствующих значений и из-за этого не попадают в доверительный интервал.
Интервальный метод применяется в тех случаях, когда данные не разнородны, иначе доверительный интервал будет включать в себя слишком большой диапазон значений, в том числе и аномальных. Для проверки степени однородности информации используют коэффициент вариации, на основе которого можно сказать, стоит ли применять данный метод или нет.
Корреляционно-регрессионный метод
Зачастую в персональной информации содержатся данные, которые взаимосвязаны между собой (например, рост и вес человека, доход и размер кредита и т.п.). В таком случае можно рассчитать количественную зависимость между этими переменными и выразить ее в виде математической формулы. Подставляя известные значения в полученное уравнение, пропущенные данные можно восстановить.
Проверка информации с помощью корреляционно-регрессионного метода делится на два этапа: расчет корреляций и расчет регрессий. Это две стадии одного и того же анализа данных.
Корреляция характеризует меру зависимости между переменными и используется для выявления взаимосвязанных значений. Для ее вычисления применяется несколько статистических коэффициентов. Приведем некоторые из них для различных типов данных:
- Коэффициент Пирсона ($r$). Вычисляется по формуле:
- Коэффициент Спирмена ($p$). Вычисляется по формуле:
$p=1- \frac{6 \times \sum (x_i-y_i)^2}{N \times(N^2-1)}$,
где
$x_i$ – ранги значений, принимаемых признаком $X$,
$y_i$ – ранги значений, принимаемых признаком $Y$,
$N$ – число пар рангов.
Обязательным условием перед вычислением коэффициента является предварительное ранжирование значений. Данный процесс приводит к тому, что значения этих рядов приобретают одинаковый минимум, равный 1 (минимальный ранг), и максимум, равный $N$ (количество данных).
При использовании коэффициента ранговой корреляции можно условно оценить взаимосвязь между переменными. Если значение коэффициента Спирмена менее 0,3, то данные почти не взаимосвязаны между собой. Значение показателя более 0,3, но менее 0,7 говорит об умеренной зависимости. При величине коэффициента Спирмена более 0,7 между данными существует сильная связь.
Коэффициент Спирмена вычисляется для ординальных данных. Его преимущество в том, что он применяется и для выявления нелинейной связи, а использование в расчетах вместо величин их рангов делает значения коэффициента менее чувствительными к выбросам.
- Коэффициент взаимной сопряженности Пирсона ($K$). Прежде чем воспользоваться формулой для расчета данного коэффициента информацию следует расположить определенным образом (таблица 7).
Таблица 7 – Таблица для анализа связи с помощью коэффициента взаимной сопряженности Пирсона
Признаки A B C Итого D $m_{11}$ $m_{12}$ $m_{13}$ $\sum m_{1j}$ E $m_{21}$ $m_{22}$ $m_{23}$ $\sum m_{2j}$ F $m_{31}$ $m_{32}$ $m_{33}$ $\sum m_{3j}$ Итого $\sum m_{i1}$ $\sum m_{i2}$ $\sum m_{i3}$ $N$ где $m_{ij}$ – совместные частоты появления двух признаков $X$ и $Y$, $N$ – число пар значений.
Коэффициент взаимной сопряженности Пирсона вычисляется по формуле:
$$K = \sqrt{\frac{\phi ^2}{1+ \phi ^2}}$$
где $\phi ^2$ – показатель средней квадратической сопряженности, который определяется по формуле:
$$\phi^2=(\frac{m^2_{11}}{\sum m_{1j}\times \sum m_{i1}}+\frac{m^2_{21}}{\sum m_{2j}\times \sum m_{12}}+\dots \frac{m^2_{33}}{\sum m_{3j}\times \sum m_{13}})-1$$
Преимущество коэффициента взаимной сопряженности Пирсона в том, что он может использоваться для расчета степени взаимосвязи между категориальными данными. Показатель изменяется от 0 до 1 и анализируется так же, как и коэффициент Спирмена.
$r=\frac{\sum \limits_{1}^{i}(x_i-\bar{x})\times (y_i-\bar{y})}{\sqrt{\sum \limits_{1}^{i} (x_t - \bar{x})^2 \times \sum \limits_{1}^{i} (y_t - \bar{y})^2}}$,
где
$x_i$ – ранги значений, принимаемых признаком $X$,
$y_i$ – ранги значений, принимаемых признаком $Y$,
$\bar{x}$ – среднее арифметическое значение по признаку $X$,
$\bar{y}$ – среднее арифметическое значение по признаку $Y$.
Коэффициент Пирсона изменяется в пределах от -1 до +1. Если он равен 0, то линейная зависимость между $x_i$ и $y_i$ отсутствует. Положительное его значение, близкое к 1, свидетельствует о существовании сильной положительной связи, т.е. рост величины $x_i$ ведет к росту величины $y_i$, а отрицательное, близкое к -1, демонстрирует противоположную тенденцию: уменьшение $y_i$ по мере увеличения $x_i$.
Коэффициент Пирсона характеризует существование линейной зависимости между несколькими переменными. Он применяется только для количественных данных. Если значения не подчиняются нормальному закону распределения или содержат аномалии, то лучше воспользоваться коэффициентом ранговой корреляции Спирмена.
После этапа корреляции, на котором происходит отбор переменных с сильной взаимосвязью, для выбранных признаков проводится регрессионный анализ. Для этого составляется регрессионная функция вида:
$Y = b_0 + b_1 \times X_1 + b_2\times X_2 +\dots+ b_n\times X_n$,
где
$b_n$ – коэффициенты регрессии, соответствующим образом подобранные для оптимального предсказывания зависимой переменной $Y$,
$X_n$ – отобранные независимые переменные,
$n$ – количество переменных.
Линия регрессии ищется с помощью метода наименьших квадратов. Его суть в том, что сумма квадратов разницы между величинами, вычисленными по уравнению, и действительными значениями должна быть минимальна. Полученное уравнение используется для оценки неверных значений. Зная функцию регрессии, в уравнение подставляют известные переменные и по ним вычисляют значение, в котором была обнаружена ошибка (аномалия или пропуск). Таким образом, данная функция позволяет заменить пропущенное значение наиболее подходящей величиной.
Пример
Как известно, между весом, ростом, полом и возрастом человека существует определенная взаимосвязь. Значит, для очистки таких полей можно использовать корреляционно-регрессионный метод.
Приведем таблицу с данными о весе, росте и возрасте женщин-респондентов (таблица 8).
Таблица 8 – Зависимость между весом, ростом и возрастом женщин-респондентов
| ФИО | Возраст | Рост | Вес |
|---|---|---|---|
| Иванова И. И. | 20 |
176 |
75 |
| Федорова Ф. Ф. | 20 |
150 |
48 |
| Петрова П. П. | 30 |
154 |
60 |
| Хворостова А. А. | 30 |
158 |
64 |
| Алексеева А. А. | 40 |
166 |
76 |
| Цаплина И. И. | 40 |
172 |
81 |
| Сидорова С. С. | 50 |
160 |
66 |
| Алешина А. А. | 50 |
182 |
86 |
| Челканова Е. Е. | 60 |
168 |
73 |
| Юлина Ю. Ю. | 60 |
156 |
- |
При заполнении анкеты Юлина Ю. Ю. неразборчиво записала информацию о своем весе. Оператор при вводе ее данных не смог определить, какая цифра должна была стоять в этом поле. С помощью корреляционно-регрессионного метода требуется восстановить пропуск в информации.
Рассчитаем с помощью аналитической платформы Deductor степень взаимосвязи между имеющимися данными на основе коэффициента Пирсона (рисунок 1).

Таким образом, из полученных значений коэффициентов следует, что взаимосвязь между ростом и весом очень сильная, а между возрастом и весом – умеренная. Значит, обе величины оказывают воздействие на вес респондентов и могут участвовать в регрессионном анализе.
Рассчитаем коэффициенты регрессии с помощью аналитической платформы Deductor. Уравнение имеет вид:
$$\mbox {weight}= -93,915+0,164 \times \mbox {age}+0,954 \times \mbox {height}$$
Сама линия регрессии, а также диаграмма рассеяния представлены на рисунке (рисунок 2).
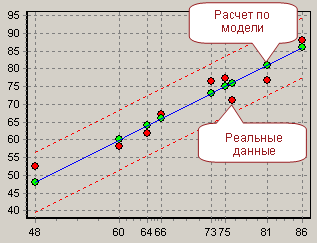
Определим вес Юлиной Ю. Ю. по формуле. Он будет равняться 65. Таким образом, используя вышеприведенную зависимость, можно оценить вес любого респондента, если он не указал его значение.
Корреляционно-регрессионный метод дает возможность восстановить данные, если они подчиняются какому-либо закону и между исследуемыми переменными существует взаимосвязь. Если же данные разнородны, то использование этого метода не приведет ни к какому результату.
Резюме
Описанные выше методы на основе статистических показателей позволяют провести качественный анализ данных и очистить "загрязненную" информацию от ошибок (опечаток, пропусков, аномалий и противоречий в данных).
Так как данные методы вычисляются с помощью статистических показателей с использованием всех имеющихся данных, то важным требованием к их применению является наличие определенных закономерностей в исследуемых сведениях. В этом случае "загрязненные" значения можно выявить и заменить наиболее подходящими, иначе правильные данные будут приняты за ошибки и тем самым исправлены на неверные величины.
В связи с этим эксперт должен контролировать процесс очистки информации. Он следит за тем, какие ошибки были найдены, стоит ли их исправлять, выбирает наиболее подходящие значения для их замены и оценивает правильность принятого решения.
В следующей статье пойдет речь о методах восстановления значений с помощью Data Mining, являющимися наиболее сложными, но эффективными средствами поиска и исправления ошибок.