Приложения вейвлет-анализа
Вейвлет-анализ является на сегодняшний день одной из самых перспективных технологий анализа данных, его инструменты находят применение в самых различных сферах интеллектуальной деятельности. Мы надеемся привлечь к этой технологии внимание специалистов в различных предметных областях.
Мы попытались осветить некоторые, самые актуальные, вопросы применения вейвлетов в наиболее общих задачах, связанных с обработкой информации, таких как очистка сигнала от помех, сжатие данных, выявление кратковременных и глобальных закономерностей, спектральный анализ составляющих сигнала.
Очистка сигнала от шума
Одна из наиболее актуальных задач цифровой обработки сигналов – задача очистки сигнала от шума. Любой практический сигнал содержит не только полезную информацию, но и следы некоторых посторонних воздействий (помехи или шум). Модель такого сигнала можно записать следующим образом:
$s(t)=f(t)+\sigma e (t)$,
где
$f(t)$ – полезный сигнал,
$s(t)$ – исследуемый сигнал,
$\sigma$ – уровень шума,
$e (t)$ – шум.
В большинстве случаев можно предположить, что функция $e (t)$ описывается моделью белого (гауссовского) шума, и информация о помехе содержится в высокочастотной области спектра сигнала, а полезная информация – в низкочастотной.
Для такой модели удаление шума при помощи вейвлет-преобразования выполняется в четыре этапа:
- Разложение сигнала по базису вейвлетов.
- Выбор порогового значения шума для каждого уровня разложения.
- Пороговая фильтрация коэффициентов детализации.
- Реконструкция сигнала.
Со статистической точки зрения такая методика представляет собой непараметрическую оценку регрессионной модели сигнала с использованием ортогонального базиса. Методика наилучшим образом работает на достаточно гладких сигналах, т.е. на сигналах, в разложении которых лишь небольшое количество коэффициентов детализации значительно отличается от нуля.
Выбор используемого вейвлета и глубины разложения, в общем случае, зависит от свойств конкретного сигнала. Можно дать лишь несколько рекомендаций:
- Более гладкие вейвлеты создают более гладкую аппроксимацию сигнала, и наоборот – "короткие" вейвлеты лучше отслеживают пики аппроксимируемой функции.
- Глубина разложения влияет на масштаб отсеиваемых деталей. Другими словами, при увеличении глубины разложения модель вычитает шум все большего уровня, пока не наступит "переукрупнение" масштаба деталей и преобразование начнет искажать форму исходного сигнала.
Интересно, что при дальнейшем увеличении глубины разложения преобразование начинает формировать сглаженную версию исходного сигнала, т.е. отфильтровывается не только шум, но и некоторые локальные особенности (выбросы) исходного сигнала.
Проиллюстрируем сказанное. На первом рисунке показан результат очистки некоторого зашумленного сигнала с помощью гладкого вейвлета (Добеши 7-го порядка, 5 уровней разложения), на втором – то же, но с использованием более короткого вейвлета (Добеши 2-го порядка, лучше отслеживаются пики сигнала), на третьем – результат "переукрупнения" сигнала (7 уровней разложения, сглаживаются локальные особенности сигнала).
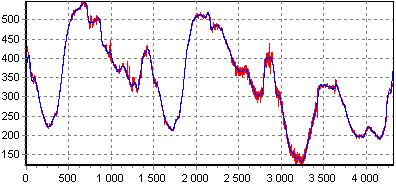
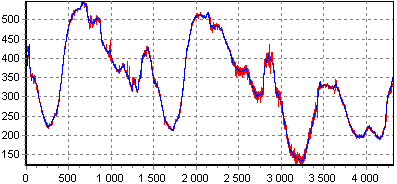
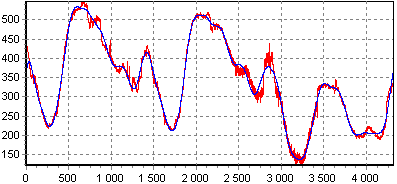
При выборе порога шума (этап 2) используют, как правило, критерии, минимизирующие квадратичную функцию потерь для выбранной модели шума. Существует множество таких критериев, и их рассмотрение выходит за рамки этой статьи. В качестве примера приведем выражение для так называемого "универсального" критерия, вполне подходящего для модели гауссовского шума с матожиданием 0 и дисперсией 1:
$\Theta = \sqrt {2 ln (n)}$,
где
$n$ – полезный сигнал,
$\Theta$ – шум.
Если уровень шума $\sigma $ (для гауссовского распределения – это среднеквадратичное отклонение) отличается от 1, то значение порога должно быть масштабировано на это величину.
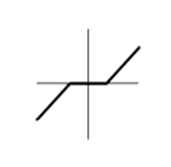
Для фильтрации коэффициентов детализации, выполняемой на третьем этапе, лучше использовать метод "мягкой" пороговой фильтрации. При этом коэффициенты, абсолютное значение которых меньше порогового, обнуляются, а остальные – "подтягиваются" к нулевому значению на величину порога:
$f(n) = \begin{cases} x+ \Theta, \,\mbox {} \, x< 0\, \mbox {} \, \left | x> 0 \right |,\\ x- \Theta,\,\mbox {} \, x> 0 \,\mbox {}\, \left | x> 0 \right |,\\ 0, \left | x \leq 0 \right | \end{cases}$
где
$x$ – значение коэффициента до фильтрации,
$y$ – значение коэффициента после фильтрации,
$\Theta$ – порог.
Сжатие сигналов
Другим полезным приложением вейвлет-анализа является сжатие информации. Принцип работы алгоритмов арифметического и статистического сжатия основывается на повышении энтропии сигнала, т.е. исключении избыточной информации. Другими словами, чем больше повторяющихся значений содержит сигнал, тем выше степень его сжатия.
Поскольку для гладких сигналов подавляющее большинство коэффициентов детализации близки к нулю, а количество коэффициентов аппроксимации экспоненциально уменьшается с повышением глубины разложения, то сжатие вейвлет-разложения сигнала потенциально более эффективно, чем сжатие исходного сигнала.
Более того, использование методики обнуления коэффициентов, подобной описанной выше, позволяет реализовать сжатие с потерями (т.е. реконструированный сигнал отличается от исходного в допустимых пределах) с еще большей эффективностью. В целом, методика сжатия сигналов с использованием вейвлет-преобразования подобна методике очистке сигнала от шума, за исключением нескольких особенностей:
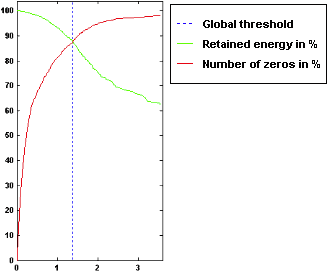
- Рекомендуется использовать другие критерии выбора порога. Например, можно использовать критерий баланса между количеством нулевых коэффициентов и остаточной энергией сигнала. Суть этого метода заключается в том, что коэффициенты детализации с абсолютным значением близким к нулю содержат лишь небольшую часть энергии сигнала.
Обнуление этих коэффициентов приводит к незначительным потерям энергии. Оптимальным является такое значение порога, при котором процент обнуляемых коэффициентов детализации будет приблизительно равен проценту остаточной энергии сигнала после пороговой фильтрации.
Повышение порога будет повышать степень сжатия, но, вместе с тем, будут расти потери качества. Понижение порога позволяет уменьшить потери при сжатии, но снижает его эффективность.
- Если сигнал не содержит крупномасштабных (низкочастотных) составляющих или их энергия невысока, то коэффициенты аппроксимации в разложении такого сигнала также будут близки к нулю. Следовательно, пороговую фильтрацию при сжатии лучше производить не для каждого уровня разложения (как при удалении шума), а для всего разложения в целом (возможно, включая и коэффициенты аппроксимации).
- Рекомендуется использовать "жесткую" пороговую фильтрацию. При этом коэффициенты, абсолютное значение которых не превышает порогового значения, обнуляются, а все остальные остаются без изменения. Такой метод фильтрации позволяет более точно восстановить резкие изменения сигнала (скачки, узкие пики и т.п.) и сохранить большее количество энергии в реконструкции сигнала.
- Вейвлет-преобразование представляет собой лишь метод первичной обработки сигнала для повышения эффективности его сжатия. Непосредственно сжатие выполняется после этой предобработки классическими методами. При этом сжатие выполняется, разумеется, для коэффициентов вейвлет-разложения сигнала, а его реконструкция по этим коэффициентам производится на этапе восстановления (декомпрессии).
Использование возможностей кратномасштабного анализа
Как уже неоднократно упоминалось, вейвлет-преобразование является инструментом кратномасштабного анализа. Напомним, что инструменты кратномасштабного анализа позволяют рассматривать исследуемый сигнал с различными масштабами: "через микроскоп", "невооруженным взглядом", "через бинокль". Такой анализ позволяет, с одной стороны, выделять кратковременные локальный особенности сигнала, незаметные на фоне его глобальных изменений. С другой стороны, можно "отфильтровать" незначительные высокочастотные изменения сигнала, сосредоточившись на изучении его глобальных, долговременных эволюций.
Выявление точек разрыва и характерных особенностей сигнала
Вейвлет-преобразование может служить своеобразным "магическим стеклом", позволяя увидеть локальные кратковременные особенности сигнала, неразличимые при его исследовании классическими методами. Примером таких особенностей являются сбои в показаниях датчиков или царапины на зеркальной поверхности.
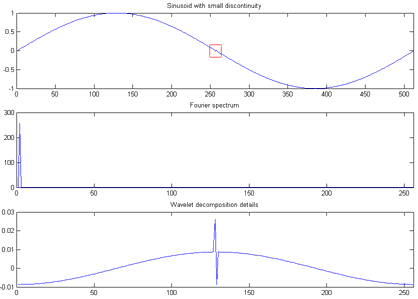
Рассмотрим синусоидальный сигнал, имеющий небольшое локальное искажение (выделено квадратом на графике). На спектрограмме сигнала эта особенность никак не отражается – видна только гармоническая составляющая. Однако на диаграмме коэффициентов детализации эта особенность выражена очень наглядно.
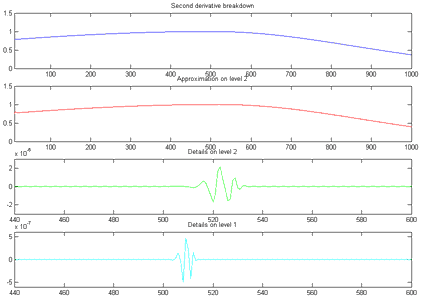
Другой пример – нарушение непрерывности второй производной сигнала. График этой функции выглядит как гладкая кривая, но на самом деле состоит из двух экспоненциальных компонентов, соединяющихся в точке t=500. Непрерывность нарушается только во второй производной, и этот момент также хорошо заметен на графике вейвлет-разложения.
Выявление долговременной эволюции
Эту задачу рассмотрим на примере монотонно возрастающей функции, сильно искаженной шумом – настолько, что это свойство практически незаметно. Однако, вейвлет-аппроксимация уже на шестом уровне преобразования достаточно наглядно показывает характер долговременного изменения функции, выделяя шум в коэффициенты детализации.

Спектральный анализ
При исследовании и обработке сигнала много полезной информации можно получить из анализа его частотных характеристик. Поскольку вейвлеты обладают хорошей частотно-временной адаптацией, они могли бы послужить удобным инструментом для исследования частотных характеристик сигнала.
Кроме того, интуитивно понятна связь между масштабом вейвлет-преобразования и его частотной областью: чем крупнее масштаб, тем более низкие частоты анализируются. Однако, для практического применения вейвлетов в спектральном анализе сигналов, необходимо установить соответствие между масштабом вейвлета и его частотными характеристиками.
Рассмотрим спектры четырех младших представителей семейства вейвлетов Добеши.
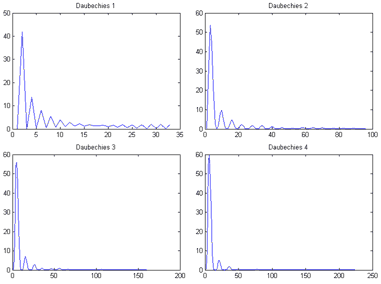
На спектрограммах ясно виден пик в низкочастотной области, в то время как амплитуда других составляющих спектра близка к нулю. Следовательно, вейвлеты являются узкополосными фильтрами и могут выделять из сигнала составляющие, частота которых соответствует их пику (эта частота называется центральной частотой вейвлета, на рисунке показаны те же четыре вейвлета и синусоиды, соответствующие их центральным частотам).
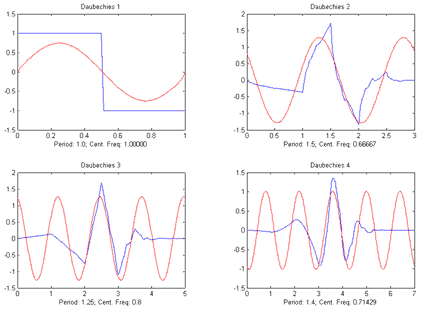
Более того, изменение масштаба вейвлета приводит к пропорциональному изменению его центральной частоты:
$F_a = \frac{\Delta \cdot F_c}{a}$,
где
$F_a$ – частота на масштабе $a$,
$F_c$ – центральная частота вейвлета на масштабе 1,
$\Delta$ – период дискретизации.
Таким образом, изменяя масштаб вейвлет-преобразования, можно перекрыть весь частотный диапазон исследуемого сигнала. А за счет хорошей временной локализации вейвлет-преобразования можно получить информацию о спектре буквально в каждой точке сигнала.
Приведем пример. Выберем семь синусоид и исследуем их при помощи вейвлета Добеши 3-го порядка. Частоту первой синусоиды (для простоты реализации) возьмем равной центральной частоте используемого вейвлета на масштабе 1, а частоты остальных составляющих будем уменьшать в 2 раза. Для определения таких составляющих масштабы тоже должны отличаться в 2 раза – следовательно, можно применить уже хорошо нам известный алгоритм быстрого вейвлет-преобразования.
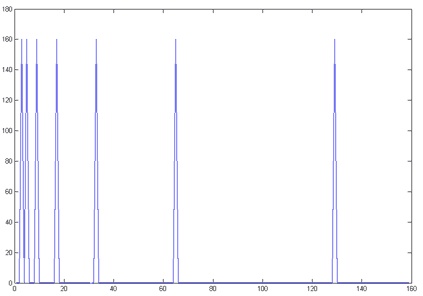
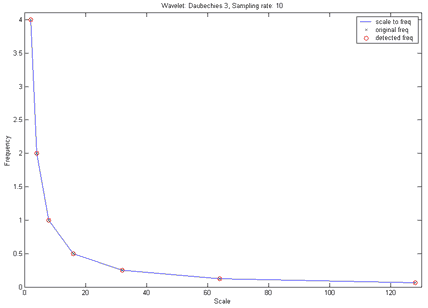
Выполним разложение каждой синусоиды до 7-го уровня, определим среднеквадратичное отклонение (СКО) коэффициентов детализации на каждом уровне разложения и выберем в качестве оценки частоту, соответствующую масштабу, имеющему наибольшее СКО. На рисунке показан график зависимости частоты от масштаба (scale to freq), частоты составляющих исходного сигнала (original freq) и частоты, определенные в результате анализа (detected freq). Стопроцентное попадание!
Заключение
Разумеется, возможности использования вейвлетов не ограничиваются перечисленными задачами. Статистическая обработка, подавление избыточной информации, криптография и стеганография, обработка мультитмедийной информации – это лишь краткая сводка тех областей, где вейвлеты находят наиболее активное применение.
В последующих статьях мы постараемся осветить хотя бы некоторые аспекты практического применения вейвлетов в предметных областях – таких как медицина, связь, прогнозирование, анализ финансовых рынков.
- Добеши, И. "Десять лекций по вейвлетам". Москва, РХД, 2001.
- Корн, Г., Корн, Т. "Справочник по математике для научных работников и инженеров". Москва, "Наука", 1977.
- Donoho, D.L. (1995), "De-Noising by soft-thresholding", IEEE Trans. on Inf. Theory, vol.41,3,pp.613-627. www-stat.stanford.edu/~donoho/
- Abry, P. (1997), Ondelettes et turbulence. Multiresolutions, algorithmes de decomposition, invariance d'echelles, Diderot Editeur, Paris.