Использование самоорганизующихся карт в задачах кластеризации
Иногда возникают задачи анализа данных, которые с трудом можно представить в математической числовой форме. Это случай, когда нужно извлечь данные, принципы отбора которых заданы нечетко: выделить надежных партнеров, определить перспективный товар и т.п. Рассмотрим типичную для задач подобного рода ситуацию – предсказание банкротств. Предположим, что у нас есть информация о деятельности нескольких десятков банков (их открытая финансовая отчетность) за некоторый период времени. По окончании этого периода мы знаем, какие из этих банков обанкротились, у каких отозвали лицензию, а какие продолжают стабильно работать (на момент окончания периода). И теперь нам необходимо решить вопрос о том, в каком из банков стоит размещать средства. Естественно, маловероятно, что мы хотим разместить средства в банке, который может скоро обанкротится. Значит, нам надо каким-то образом решить задачу анализа рисков вложений в различные коммерческие структуры.
На первый взгляд, решить эту проблему несложно – ведь у нас есть данные о работе банков и результат их деятельности. Но, на самом деле, эта задача не так проста. При этом возникает проблема, связанная с тем, что имеющиеся у нас данные описывают прошедший период, а нас интересует то, что будет в дальнейшем. Таким образом нам надо на основании имеющихся у нас априорных данных получить прогноз на дальнейший период. Для решения этой задачи можно использовать различные методы.
Так, например, наиболее очевидным является применение методов математической статистики. Но тут возникает проблема с количеством данных, ибо статистические методы хорошо работают при большом объеме априорных данных, а у нас может быть ограниченное их количество. При этом статистические методы не могут гарантировать успешный результат.
Другим путем решения этой задачи может быть применение нейронных сетей, которые можно обучить на имеющемся наборе данных. В этом случае в качестве исходной информации используются данные финансовых отчетов различных банков, а в качестве целевого поля – итог их деятельности.
Но при использовании описанных выше методов мы навязываем результат, не пытаясь найти закономерности в исходных данных. В принципе все обанкротившиеся банки похожи друг на друга хотя бы тем, что они обанкротились. Значит, в их деятельности должно быть что-то более общее, что привело их к этому итогу. Значит, можно попытаться найти эти закономерности с тем, чтобы использовать их в дальнейшем. И тут перед нами возникает вопрос о том, как найти эти закономерности. Для этого, если мы будем использовать методы статистики, нам надо определить, какие критерии "похожести" нам использовать, что может потребовать от нас каких-либо дополнительных знаний о характере задачи.
Однако существует метод, позволяющий автоматизировать все эти действия по поиску закономерностей – метод анализа с использованием самоорганизующихся карт Кохонена. Рассмотрим, как решаются такие задачи и как карты Кохонена находят закономерности в исходных данных. Для общности рассмотрения будем использовать термин объект (например, объектом может быть банк, как в рассмотренном выше примере, но описываемая методика без изменений подходит для решения и других задач – например, анализа кредитоспособности клиента, поиска оптимальной стратегии поведения на рынке и т.д.).
Каждый объект характеризуется набором различных параметров, которые описывают его состояние. Например, для нашего примера параметрами будут данные из финансовых отчетов. Эти параметры часто имеют числовую форму или могут быть приведены к ней.
Таким образом нам надо на основании анализа параметров объектов выделить схожие объекты и представить результат в форме, удобной для восприятия.
Все эти задачи решаются самоорганизующимися картами Кохонена. Рассмотрим подробнее, как они работают. Для упрощения рассмотрения будем считать, что объекты имеют 3 признака (на самом деле их может быть любое количество).
Теперь представим, что все эти три параметра объектов представляют собой их координаты в трехмерном пространстве (в том самом пространстве, которое окружает нас в повседневной жизни). Тогда каждый объект можно представить в виде точки в этом пространстве, что мы и сделаем (чтобы у нас не было проблем с различным масштабом по осям, пронормируем все эти признаки в интервал [0,1] любым подходящим способом), в результате чего все точки попадут в куб единичного размера. Отобразим эти точки (см. рис. 1).
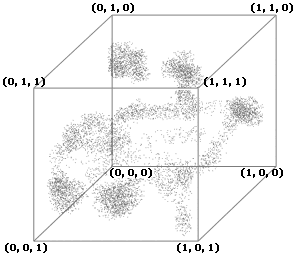
Взглянув на этот рисунок, мы можем увидеть, как расположены объекты в пространстве, причем легко заметить участки, где объекты группируются, т.е. у них схожи параметры, значит, и сами эти объекты, скорее всего, принадлежат одной группе. Но так легко можно поступить только в случае, когда признаков немного (так, например, я не знаю, как можно изобразить четырехмерное пространство). Значит, нам надо найти способ, которым можно преобразовать данную систему в простую для восприятия, желательно двумерную систему (потому что уже трехмерную картинку невозможно корректно отобразить на плоскости) так, чтобы соседние в искомом пространстве объекты оказались рядом и на полученной картинке. Для этого используем самоорганизующуюся карту Кохонена. В первом приближении ее можно представить в виде сети, изготовленной из резины (см. рис. 2).
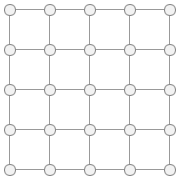
Мы, предварительно "скомкав", бросаем эту сеть в пространство признаков, где у нас уже имеются объекты, и далее поступаем следующим образом: берем один объект (точку в этом пространстве) и находим ближайший к нему узел сети. После этого этот узел подтягивается к объекту (т.к. сетка "резиновая", то вместе с этим узлом так же, но с меньшей силой подтягиваются и соседние узлы). Затем выбирается другой объект (точка), и процедура повторяется. В результате мы получим карту, расположение узлов которой совпадает с расположением основных скоплений объектов в исходном пространстве. Кроме того, полученная карта обладает следующим замечательным свойством – узлы ее расположились таким образом, что объектам, похожим между собой соответствуют соседние узлы карты (см. рис.3). Теперь определяем, какие объекты у нас попали в какие узлы карты. Это также определяется ближайшим узлом – объект попадает в тот узел, который находится ближе к нему. В результате всех этих операций объекты со схожими параметрами попадут в один узел или в соседние узлы. Таким образом можно считать, что мы смогли решить задачу поиска похожих объектов и их группировки.
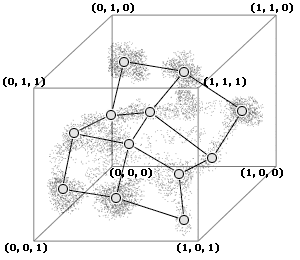
Но на этом возможности карт Кохонена не заканчиваются. Они позволяют также представить полученную информацию в простой и наглядной форме путем нанесения раскраски. Для этого мы раскрашиваем полученную карту (точнее ее узлы) цветами, соответствующими интересующим нас признакам объектов. Возвращаясь к примеру с классификацией банков, можно раскрасить одним цветом те узлы, куда попал хоть один из банков, у которых была отозвана лицензия. Тогда после нанесения раскраски мы получим зону, которую можно назвать зоной риска, и попадание интересующего нас банка в эту зону говорит о его ненадежности.
Но и это еще не все. Мы можем также получить информацию о зависимостях между параметрами. Нанеся на карту раскраску, соответствующую различным статьям отчетов, можно получит так называемый атлас, хранящий в себе информацию о состоянии рынка. При анализе, сравнивая расположение цветов на раскрасках, порожденных различными параметрами, можно получить полную информацию о финансовом портрете банков – неудачников, процветающих банков и т.д.
При всем этом описанная технология является универсальным методом анализа. С ее помощью можно анализировать различные стратегии деятельности, производить анализ результатов маркетинговых исследований, проверять кредитоспособность клиентов и т.д.
Таким образом, имея перед собой карту и зная информацию о некоторой из части исследуемых объектов, мы можем достаточно достоверно судить об объектах, с которыми мы мало знакомы. Нужно узнать, что из себя представляет новый партнер? Отобразим его на карте и посмотрим на соседей. В результате, можно извлекать информацию из базы данных, основываясь на нечетких характеристиках.