Ядро OLAP системы. Часть 3 — построение срезов куба
Итак, в предыдущей статье мы описали способ хранения данных в виде гиперкуба. Он позволяет сформировать набор точек в многомерном пространстве на основе информации, находящейся в хранилище данных. Для того, чтобы человек мог иметь возможность работы с этими данными, их необходимо представить в виде, удобном для обработки. При этом в качестве основных видов представления данных используются сводная таблица и графики. Причем оба этих способа фактически представляют собой проекции гиперкуба. Для того, чтобы обеспечить максимальную эффективность при построения представлений, будем отталкиваться от того, что представляют собой эти проекции. Начнем рассмотрение со сводной таблицы, как с наиболее важной для анализа данных. Структура сводной таблицы достаточно подробно была рассмотрена в первой статье, посвященной разработке OLAP системы.
Найдем способы реализации такой структуры. Можно выделить три части, из которых состоит сводная таблица: это заголовки строк, заголовки столбцов и собственно таблица агрегированных значений фактов. Самым простым способом представления таблицы фактов будет использование двумерного массива, размерность которого можно определить, построив заголовки. К сожалению, самый простой способ будет самым неэффективным, потому что таблица будет сильно разреженной, и память будет расходоваться крайне неэффективно, в результате чего можно будет строить только очень малые кубы, так как иначе памяти может не хватить. Таким образом, нам необходимо подобрать для хранения информации такую структуру данных, которая обеспечит максимальную скорость поиска/добавления нового элемента и в то же время минимальный расход оперативной памяти. Этой структурой будут являться так называемые разреженные матрицы, про которые более подробно можно прочесть у Кнута. Возможны различные способы организации матрицы. Для того, чтобы выбрать подходящий нам вариант, рассмотрим изначально структуру заголовков таблицы.
Заголовки имеют четкую иерархическую структуру, поэтому естественно будет предположить для их хранения использовать дерево. При этом схематически структуру узла дерева можно изобразить следующим образом:
| Родительский узел | Значение измерения | N (Количество дочерних узлов) | Столбец (строка) со значением |
|---|---|---|---|
Дочерний узел 1 |
Дочерний узел 2 |
... |
Дочерний узел N |
При этом в качестве значения измерения логично хранить ссылку на соответствующий элемент таблицы измерений многомерного куба . Это позволит сократить затраты памяти для хранения среза и ускорить работу. В качестве родительских и дочерних узлов также используются ссылки. Тогда описанную структуру можно реализовать следующим пседокодом:
PHeaderTreeNode = ^THeaderTreeNode;
THeaderTreeNode = record
Parent: PHeaderTreeNode; // родительский узел
Value: PDimensionRecord; // значение измерения
ChildCount: integer; // кол-во детей узла
Childs: array of PHeaderTreeNode; // массив детей узла
...
End;
В этом коде пока не указан один элемент – столбец (строка) со значением. О том, чем является это поле, мы поговорим попозже. А теперь перейдем к добавлению элементов в дерево заголовков. Каждый уровень дерева будет соответствовать одному измерению в том порядке, в котором они используются для построения среза. При этом самый верхний узел дерева будет соответствовать полному итогу в сводной таблице.
Для добавления элемента в дерево необходимо иметь информацию о его местоположении в гиперкубе. В качестве такой информации надо использовать его координату, которая хранится в словаре значений измерения (см. предыдущую статью). Рассмотрим схему добавления элемента в дерево заголовков сводной таблицы. При этом в качестве исходной информации используем значения координат измерений. Порядок, в котором эти измерения перечислены, определяется требуемым способом агрегирования и совпадает с уровнями иерархии дерева заголовков. В результате работы необходимо получить список столбцов или строк сводной таблицы, в которые необходимо осуществить добавление элемента.
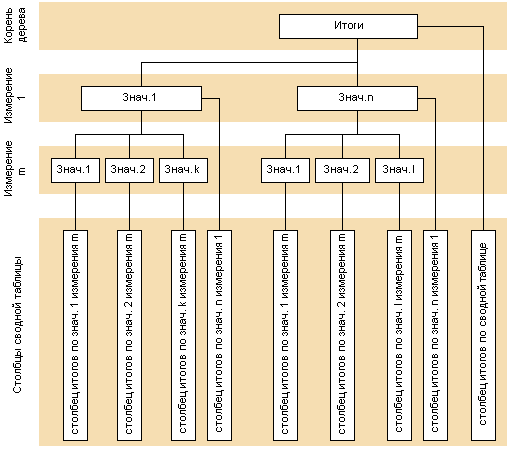
В качестве исходных данных для определения этой структуры используем координаты измерений. Кроме того, для определенности, будем считать, что мы определяем интересующий нас столбец в матрице (как будем определять строку рассмотрим чуть позже, так как там удобнее применять другие структуры данных, причина такого выбора также см. ниже). В качестве координат возьмем целые числа – номера значений измерений, которые можно определить так, как описано в предыдущей статье. Тогда это можно реализовать процедурой, имеющей следующий вид:
Procedure GetMatrixCol(InpCoord: array of integer; var OutCols: array of PMatrixCol);
// InpCoord – набор значений координат измерений
// OutCols – набор столбцов, в формировании значений которых используется данный
// факт
Var
xNode: PheaderTreeNode; // текущий узел дерева
I: integer; // Номер текущего уровня дерева
Begin
xNode := RootNode; // присваиваем значение текущего узла в корневой узел
for I := 0 to DimensionsCols.Count – 1 do
begin
OutCols[I] := xNode.MatrixCol; // это ссылка на столбец матрицы
// проверяем, есть ли у нас соответствующий дочерний узел
if xNode.Childs[InpCoord [I]] = nil then
begin
inc(xNode).ChildCount; // увеличиваем счетчик потомков узла
// теперь создаем новый узел – потомок
xNode.Childs[InpCoord [I]] := new(TColHeaderTreeNode);
SetLength(xNode.Childs[InpCoord [I]].Childs, DimensionsCols[I].Count);
xNode.Childs[InpCoord [I]].ChildCount := 0;
xNode.Childs[InpCoord [I]].Parent := xNode;
xNode.Childs[InpCoord [I]].Value := DimensionCols[I].Value[InpCoord [I]];
end;
// переходим к следующему узлу
xNode := xNode.Childs[InpCoord [I]];
end;
End;
Итак, после выполнения этой процедуры получим массив ссылок на столбцы разреженной матрицы. Теперь необходимо выполнить все необходимые действия со строками. Для этого внутри каждого столбца необходимо найти нужный элемент и добавить туда соответствующее значение. Из того, что раньше не рассматривалось в процедуре встречается DimensionCols – это коллекция измерений, которые отложены в столбцах сводной таблицы. Для каждого из измерений в коллекции необходимо знать количество уникальных значений и собственно набор этих значений.
Теперь рассмотрим, в каком виде необходимо представить значения внутри столбцов – то есть как определить требуемую строку. Для этого можно использовать несколько подходов. Самым простым было бы представить каждый столбец в виде вектора, но так как он будет сильно разреженным, то память будет расходоваться крайне неэффективно. Чтобы избежать этого, применим структуры данных, которые обеспечат большую эффективность представления разреженных одномерных массивов (векторов). Самой простой из них будет обычный список, одно- или двусвязный, однако он неэкономичен с точки зрения доступа к элементам. Поэтому будем использовать дерево, которое обеспечит более быстрый доступ к элементам. Например, можно использовать точно такое же дерево, как и для столбцов, но тогда пришлось бы для каждого столбца заводить свое собственное дерево, что приведет к значительным накладным расходам памяти и времени обработки. Поступим чуть хитрее – заведем одно дерево для хранения всех используемых в строках комбинаций измерений, которое будет идентично вышеописанному, но его элементами будут не указатели на строки (которых нет как таковых), а их индексы, причем сами значения индексов нас не интересуют и используются только как уникальные ключи. Затем эти ключи будем использовать для поиска нужного элемента внутри столбца. Сами же столбцы проще всего представить в виде обычного двоичного дерева. Графически полученную структуру можно представить следующим образом:
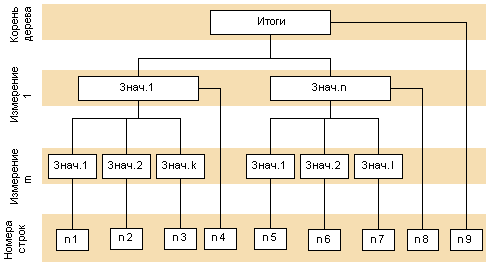
Для определения соответствующих номеров строк можно использовать такую же процедуру, что и описанная выше процедура определения столбцов сводной таблицы. При этом номера строк являются уникальными в пределах одной сводной таблицы и идентифицируют элементы в векторах, являющихся столбцами сводной таблицы. Наиболее простым вариантом генерации этих номеров будет ведение счетчика и инкремент его на единицу при добавлении нового элемента в дерево заголовков строк. Сами эти вектора столбцов проще всего хранить в виде двоичных деревьев, где в качестве ключа используется значение номера строки. Кроме того, возможно также и использование хеш-таблиц. Так как процедуры работы с этими деревьями детально рассмотрены в других источниках, то останавливаться на этом не будем и рассмотрим общую схему добавления элемента в столбец.
В обобщенном виде последовательность действий для добавления элемента в матрицу можно описать следующим образом:
- Определить номера строк, в которые добавляются элементы
- Определить набор столбцов, в которые добавляются элементы
- Для всех столбцов найти элементы с нужными номерами строк и добавить к ним текущий элемент (добавление включает в себя подсоединение нужного количества значений фактов и вычисление агрегированных значений, которые можно определить инкрементально).
После выполнения этого алгоритма получим матрицу, представляющую собой сводную таблицу, которую нам было необходимо построить.
Теперь пара слов про фильтрацию при построении среза. Проще всего ее осуществить как раз на этапе построения матрицы, так как на этом этапе имеется доступ ко всем требуемым полям, и, кроме того, осуществляется агрегация значений. При этом, во время получения записи из кэша, проверяется ее соответствие условиям фильтрации, и в случае его несоблюдения запись отбрасывается.
Так как описанная выше структура полностью описывает сводную таблицу, то задача ее визуализации будет тривиальна. При этом можно использовать стандартные компоненты таблицы, которые имеются практически во всех средствах программирования под Windows.