Ассоциативная память — применение сетей Хемминга для нечеткого поиска

Методология0 комментариевВерсия для печати

Принцип работы памяти у компьютера Фон-Неймановской архитектуры и человека принципиально отличаются друг от друга. Компьютер используется для поиска информации адрес, а человек ассоциации. Поэтому, если вы знаете, где искать информацию, компьютер найдет ее быстро, но если не знаете, то придется все перебирать. Хорошо еще, если данные не искажены. Вероятно, более "качественная" (если можно так выразиться) память человека позволяет при гораздо меньших вычислительных возможностях лучше анализировать. Принципиальную ограниченность современных компьютеров можно обойти при помощи различного рода систем ассоциативной памяти, например, сетей Хемминга.

Принципы работы сетей Хемминга

Алгоритм работы базируется на определении Хеммингово расстояния. Хеммингово расстояния – это количество отличающихся позиций в бинарных векторах. Результатом работы сети является нахождение образа с наименьшим расстоянием.

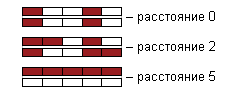
Отсутствие сигнала кодируется как (-1), наличие (1). Сеть состоит всего из 2-х слоев.

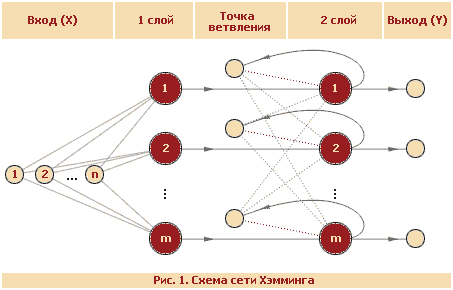
Алгоритм работы

1. Инициализация весовых коэффициентов первого слоя.
   $w_{ij} = \frac{x_i^j}{2},i = 0\dots n-1,j = 0\dots m-1$,
   где Х – запоминаемые образы, i – соответствующий компонент вектора X, j – номер образа, n – размерность вектора X, m – количество запоминаемых образов.
2. Расчет состояния нейронов первого слоя.
   $y_j^{(1)} = s_j^{(1)} = \sum \limits_{i=0}^{n-1}\,w_{ij}\,x_i\,+\,T_j$,
   где X – неизвестный образ, T = n/2 – порог активационной функции
3. Расчет состояния нейронов второго слоя.
   $s_j^{(2)}\,(p\,+\,1) = y_i\,(p)\,-\,\varepsilon\sum\limits_{k=0}^{m-1}\,y_k^{(2)}\,(p),\,k\,\neq\,j,\,j=0\,\dots\,m-1,$,
   где p – номер итерации, 0 < < 1/m
   $y_j^{(2)}\,(p\,+\,1) = f\,\Bigl[s_j^{(2)}\,(p\,+\,1)\Bigr],\,j=0\,\dots\,m-1$,
   где f – пороговая активационная функция.
   $f(x) = \begin{cases} {0,x}<{0}\\ {x,0}\leq x <{F}\\ {F,x} \geq F \end{cases}$,
   где F – порог активационной функции. Обычно F выбирается достаточно большим, так, чтобы при любом допустимом значении входа не наступало насыщение. На практике F обычно берется равным количеству примеров.
4. Проверка условия выхода.
   Если выходы не стабилизировались, т.е. изменялись за последнюю итерацию, то переход на шаг 3, иначе конец.

Область применения

На ум сразу приходит задача оптического распознавания символов (OСR). Действительно, так оно и есть. При решении этой задачи сети Хемминга активно используются. Но это, так сказать, лежит на поверхности. На практике они используются для восстановления зашумленного исходного сигнала, задачах оптимизации и во многих других случаях. Рассмотрим один из таких частных случаев – нечеткий поиск.

Итак, у нас на входе словарь, необходимо найти искомое слово в этом словаре, даже если оно было набрано с ошибкой. Для этого нужно сначала придумать систему кодирования символьной информации в вектора. Зададим для каждого символа его битовую маску.

А – 00001
Б – 10001
В – 10010
…

Хотелось бы обратить внимание, что при кодировании желательно учитывать источник получения информации. Например, если для ввода информации используется клавиатура, то лучше всего было бы задавать коды символов таким образом, чтобы у символов, расположенных рядом на клавиатуре, были бы и близкие по Хеммингу коды. Если же источником является OCR программа, то близкие коды должны быть у схожих по написанию символов. После кодирования таким образом подаем полученные вектора на вход нейросети.

Тут необходимо учитывать одну особенность сетей Хемминга. Если при написании была опечатка или даже две, то алгоритм работает хорошо, но если был пропущен символ или добавлен лишний, то Хемингово расстояние может оказаться слишком большим. Для того, чтобы сгладить этот недостаток, мы будем подавать на вход как само искомое слово, так и это же слово, исключая по очереди по одному символу в каждой позиции и добавляя по одной букве в каждую позицию. Такой подход позволит найти практически все случаи ошибок – опечатка, пропуск символа, лишний символ.