Область применения
При работе над прогнозированием временных рядов, обычно производится разработка нескольких возможных статистических моделей исследуемого процесса и из них необходимо выбрать наиболее обоснованную и соответствующую ситуации.
Описание
Характеристики качества информационной пригодности моделей прогнозирования описывают, на сколько достоверно, выбранная в качестве генератора прогноза, модель описывает ретроспективу исследуемого явления. Чем точнее построенная модель объясняла прошлое, тем больше вероятность того, что она будет удачно предсказывать будущее. Надежность моделей прогнозирования оценивается путем сравнения фактических и предсказанных значений. Эта разница позволяет проверить, применима ли к конкретным данным рассматриваемая модель и те предположения, на которых она основана. Основными оценочными характеристиками качества прогнозной модели являются нижеследующие показатели.
- Модельная погрешность (модельный остаток):
$e_t=y_t-y_t^{sim}$, (1)
где
$y_t$ — фактическое значение показателя на момент времени; $t$-й момент времени,
$y_t^{sim}$ — значение показателя, полученное с помощью модели, на $t$-й момент времени.
- Абсолютная ошибка прогноза:
$\Delta _t=\left | y_t - y_t ^{sim} \right |$, (2)
- Средняя абсолютная ошибка прогноза $MAE$ (the mean absolute error):
$MAE=\frac{1}{n} \sum \limits_{t=1}^{n} \left | \varepsilon_t \right |$, (3)
где
$n$ — число ретроспективных наблюдений..
- Среднеквадратичное отклонение $RMSE$ (the root mean squared error):
$\sqrt{\frac{\sum \limits_{t=1}^{n} e_t^2}{n-1}}$, (4)
Однако у этого способа есть несколько особенностей, например, большая чувствительность к большим отклонениям прогнозируемого значения от реального. Пусть построенная модель в целом довольно хорошо повторяет реальные данные о продажах, но имеются несколько точек, где отклонение от реальных данных большое. Рассчитывая для модели среднеквадратическую ошибку, в таком случае оценка качества модели может быть неудовлетворительной, и в результате принимается неправильное решение при выборе модели. Для устранения этого недостатка необходимо компенсировать величину ошибки значимостью этой ошибки. В таком случае возможность перевеса множества мелких ошибок одной крупной удастся избежать.
- $MPE$ – mean percentage error, средний процент ошибки:
$MPE = \frac{1}{n} \sum \limits_{t=1}^{n}\frac{e_t}{y_t}\times 100\%$, (5)
$MPE$ характеризует относительную степень смещенности прогноза. При условии, что потери при прогнозировании, связанные с завышением фактического будущего значения, уравновешиваются занижением, идеальный прогноз должен быть несмещенным, и обе меры должны стремиться к нулю. Средняя процентная ошибка не определена при нулевых данных и не должна превышать 5%.
- Относительная ошибка прогноза:
$\varepsilon_t=\frac{\left | \varepsilon_t \right |}{y_t} \times 100\%$, (6)
- $MAPE$ – the mean absolute percentage error, средний абсолютный процент ошибки (средняя относительная ошибка прогноза):
$MAPE=\frac{1}{n}\sum \limits_{t=1}^{n}\varepsilon _t$, (7)
Отрицательные и положительные ошибки подавляют друг друга, поэтому для оценки качества построенной модели необходимо использовать среднюю абсолютную относительную ошибку.
- Абсолютное отклонение от средней:
$AD=\sum \limits_{t=1}^{n}\left | y_t - \bar {y_t} \right |$, (8)
- Среднее абсолютное отклонение $MAD$ (mean absolute deviation):
$MAD=\frac{1}{n}\sum \limits_{t=1}^{n}\left | y_t - \bar {y_t} \right |$, (9)
- $R^2$ — коэффициент детерминации. Характеризует степень сходства исходных данных и предсказанных. Не зависит от единиц измерения данных, поэтому поддается сравнению. Рассчитывается коэффициент по следующей формуле:
$R^2=\frac{{\sum \limits_{t=1}^{n}(y_t^{sim} - \bar {y})}^2}{\sum \limits_{t=1}^{n}(y_t - \bar {y})^2}= 1 - \frac{{\sum \limits_{t=1}^{n}(y_t - y_t^{sim})}^2}{\sum \limits_{t=1}^{n}(y_t - \bar {y})^2}$, (10)
Если ${R^2}=0$, это означает, что регрессия ничего не дает, т.е. знание $x$ не улучшает предсказания для $y$ по сравнению с тривиальным
 . Другой крайний случай ${R^2}=1$ означает точную подгонку: все точки наблюдений лежат на регрессионной прямой. Чем ближе к $1$ значение $R^2$, тем лучше качество подгонки.
. Другой крайний случай ${R^2}=1$ означает точную подгонку: все точки наблюдений лежат на регрессионной прямой. Чем ближе к $1$ значение $R^2$, тем лучше качество подгонки. - Коэффициент несоответствия Тейла:
$v=\sqrt{\frac{{\sum \limits_{t=1}^{n} (y_t - y_t^{sim})}^2}{{\sum \limits_{t=1}^{n} y_t^2 + \sum \limits_{t=1}^{n} y_t^{sim}}^2}}$, (11)
Индекс Тейла показывает степень схожести временных рядов $y_t$ и $y_t^{sim}$, и чем ближе он к нулю, тем ближе сравниваемые ряды.
Алгоритм
- Вычислить модельную погрешность $e_t$ по формуле (1).
- Вычислить абсолютную ошибку прогноза по формуле (2).
- Вычислить среднюю абсолютную ошибку прогноза $MAE$ по формуле (3).
- Вычислить среднеквадратичное отклонение $RMSE$ по формуле (4).
- Вычислить относительную ошибку прогноза по формуле (6).
- Вычислить среднюю относительную ошибку прогноза $MAPE$ по формуле (7). Показатель $MAPE$, как правило, используется для сравнения точности прогнозов разнородных объектов прогнозирования, поскольку он характеризует относительную точность прогноза. Для прогнозов высокой точности $MAPE<10\%$, хорошей – $10\%<\mbox {MAPE}<20\%$, удовлетворительной – $\mbox {MAPE}>50\%$. Целесообразно пропускать значения ряда, для которых $y_t=0$.
- Вычислить абсолютное отклонение от средней по формуле (8).
- Вычислить коэффициент детерминации по формуле (10).
- Вычислить коэффициент несоответствия Тейла по формуле (11).
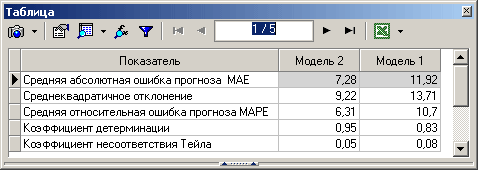
- По полученным значениям определить лучшую модель прогнозирования.
Требования к данным
| Имя поля | Метка поля | Тип данных | Вид данных |
|---|---|---|---|
| Date | Дата | Дата/Время | Непрерывный |
| Quantity | Количество | Вещественный | Непрерывный |
| Prediction_model_1 | Значение модели 1 | Вещественный | Непрерывный |
| Prediction_model_2 | Значение модели 2 | Вещественный | Непрерывный |
Сценарий