Деревья решений — CART математический аппарат. Часть 2
Эта статья является продолжением описания алгоритма CART. В первой части мы рассмотрели процесс построения дерева и процесс получения последовательности уменьшающихся поддеревьев методом cost-complexity pruning.
Итак, мы имеем последовательность деревьев, нам необходимо выбрать лучшее дерево из неё. То, которое мы и будем использовать в дальнейшем. Отметим, что отсечение дерева не использовало никаких других данных, кроме тех, на которых строилось первоначальное дерево. Даже не сами данные требовались, а количество примеров каждого класса, которое 'прошло' через узел.
Наиболее очевидным и возможно наиболее эффективным является выбор финального дерева посредством тестирования на тестовой выборке. Естественно, качество тестирования во многом зависит от объема тестовой выборки и 'равномерности' данных, которые попали в обучающую и тестовую выборки.
Часто можно наблюдать, что последовательность деревьев дает ошибки близкие друг к другу. Случай изображен на рис. 3.
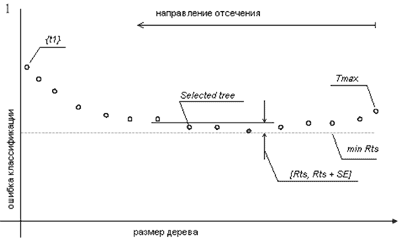
Эта длинная плоская последовательность очень чувствительна к данным, которые будут выбраны в качестве тестовой выборки. Чтобы уменьшить эту нестабильность CART использует 1-SE правило: выберите минимальное по размеру дерево с $R^{ts}$ в пределах интервала $[/min R^{ts}, /min /min R^{ts} + SE]$. $R^{ts}$ – ошибка классификации дерева. $SE$ – стандартная ошибка, являющаяся оценкой реальной ошибки.
$$SE\,(R^{ts}) = \sqrt {\frac{R^{ts}\,(1\,-\,R^{ts})}{n_{test}}}$$Где $n_{test}$ – число примеров в тестовой выборке. Ситуация проиллюстрирована на рис. 3.
Перекрестная проверка
Перекрестная проверка (V-fold cross-validation) – самая оригинальная и сложная часть алгоритма CART. Этот путь выбора финального дерева используется, когда набор данных для обучения мал или каждая запись в нем по своему 'уникальна' так, что мы не можем выделить выборку для обучения и выборку для тестирования.
В таком случае строим дерево на всех данных, вычисляем $\alpha_1,\,\alpha_2,\,\dots,\,\alpha_k$ и $T_1 > T_2 > \dots > T_N$. Обозначим $T_k$ – наименьшее минимизируемое поддерево для $[\alpha_k,\,\alpha_{k+1}]$.
Теперь мы хотим выбрать дерево из последовательности, но уже использовали все имеющиеся данные. Хитрость в том, что мы собираемся вычислить ошибку дерева $T_K$ из последовательности косвенным путем.
Шаг 1.
Установим
$$\beta_1 = 0,\,\beta_2 = \sqrt{\alpha_2\,\alpha_3},\,\beta_3 = \sqrt{\alpha_3\,\alpha_4},\,\dots,\,\beta_{N-1} = \sqrt{\alpha_{N-1}\,\alpha_N},\beta_N = \infty$$
Считается, что $\beta_k$ будет типичным значением для $[\alpha_k,\,\alpha_{k+1}]$ и, следовательно, как значение соответствует $T_K$.
Шаг 2.
Разделим весь набор данных на $V$ групп одинакового размера $G_1, G_2, \dots, G_V$. Бриман рекомендует брать $V = 10$. Затем для каждой группы $G_i$:
- Вычислить последовательность деревьев с помощью описанного выше механизма отсечения на всех данных, исключая $G_i$. И определить $T^{(i)}\,(\beta_1),\,T^{(i)}\,(\beta_2),\,\dots,\,T^{(i)}\,(\beta_N)$ для этой последовательности.
- Вычислить ошибку дерева $T^{(i)}\,(\beta_k)$ на $G_i$.
Здесь $T^{(i)}\,(\beta_k)$ означает наименьшее минимизированное поддерево из последовательности, построенное на всех данных, исключая $G_i$, для $\beta_k$.
Шаг 3.
Для каждого $\beta_k$ суммировать ошибку $T^{(i)}\,(\beta_k)$ по всем $G_i(i = 1,\dots, V)$. Пусть $\beta_h$ будет с наименьшей общей ошибкой. Так как $\beta_h$ соответствует дереву $T_h$, мы выбираем $T_h$ из последовательности построенной на всех данных в качестве финального дерева. Показатель ошибки, вычисленный с помощью перекрестной проверки можно использовать как оценку ошибки дерева.
Альтернативный путь – чтобы выбрать финальное дерево из последовательности на последнем шаге можно опять использовать 1-SE правило.
Алгоритм обработки пропущенных значений
Большинство алгоритмов Data Mining предполагает отсутствие пропущенных значений. В практическом анализе это предположение часто является неверным. Вот только некоторые из причин, которые могут привести к пропущенным данным:
- Респондент не желает отвечать на некоторые из поставленных вопросов;
- Ошибки при вводе данных;
- Объединение не совсем эквивалентных наборов данных.
Наиболее общее решение – отбросить данные, которые содержат один или несколько пустых атрибутов. Однако это решение имеет свои недостатки:
- Смещение данных. Если выброшенные данные лежат несколько 'в стороне' от оставленных, тогда анализ может дать предубеждённые результаты.
- Убыток мощности. Может возникнуть ситуация, когда придется выбросить много данных. В таком случае точность прогноза сильно уменьшается.
Если мы хотим строить и использовать дерево на неполных данных нам необходимо решить следующие вопросы:
- Как нам определить качество разбиения?
- В какую ветвь нам необходимо послать наблюдение, если пропущена переменная, на которую приходится наилучшее разбиение (построение дерева и тренировка)?
Заметьте, что наблюдение с пропущенной меткой класса бесполезно для построения дерева и будет выброшено.
Чтобы определить качество разбиения CART просто игнорирует пропущенные значения. Это 'решает' первую проблему, но мы ещё должны решить, по какому пути посылать наблюдение с пропущенной переменной содержащей наилучшее разбиение. С этой целью CART вычисляет так называемое 'суррогатное' разбиение. Оно создает наиболее близкие к лучшему подмножества примеров в текущем узле. Чтобы определить значение альтернативного разбиения как суррогатного мы создаем кросс-таблицу (см. табл. 1).
| p(l*, l') | p(l*, r') |
| p(r*, l') | p(r*, r') |
В этой таблице p(l*,l') обозначает пропорцию случаев, которые будут посланы в левую ветвь при лучшем s* и альтернативном разбиении s' и аналогично для p(r*,r'), так p(l*,l') + p(r*,r') – пропорция случаев, которые посланы в одну и ту же ветвь для обоих разбиений. Это мера сходства разбиений или иначе: это говорит, насколько хорошо мы предсказываем путь, по которому послан случай наилучшим разбиением, смотря на альтернативное разбиение. Если p(l*,l') + p(r*,r') < 0.5, тогда мы можем получить лучший суррогат, поменяв левую и правую ветви для альтернативного разбиения. Кроме того, необходимо заметить, что пропорции в таблице 1 вычислены, когда обе переменные (суррогатная и альтернативная) наблюдаемы.
Альтернативные разбиения с p(l*,l') + p(r*,r') > max(p(l*), p(r*)) отсортированы в нисходящем порядке сходства. Теперь если пропущена переменная лучшего разбиения, тогда используем первую из суррогатных в списке, если пропущена она, тогда следующую т.д. Если пропущены все суррогатные переменные, используем max(p(l*), p(r*)).
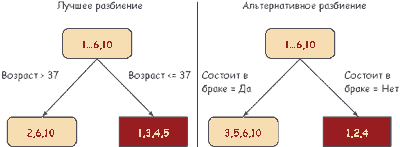
На рис. 4 изображен пример лучшего и альтернативного разбиения. Каково значение альтернативного разбиения по супружескому статусу как суррогатного? Видно, что примеры 6 и 10 оба разбиения послали влево. Следовательно p(l*,l') = 2/7. Оба разбиения послали примеры 1 и 4 направо – p(r*,r') = 2/7. Его значение как суррогатного есть p(l*,l') + p(r*,r') = 2/7 + 2/7 = 4/7. Так как max(p(l*), p(r*)) = 4/7, поэтому разбиение по супружескому статусу не является хорошим суррогатным разбиением.
Регрессия
Построение дерева регрессии во многом схоже с деревом классификации. Сначала мы строим дерево максимального размера, затем обрезаем дерево до оптимального размера.
Основное достоинство деревьев по сравнению с другими методами регрессии – возможность работать с многомерными задачами и задачами, в которых присутствует зависимость выходной переменной от переменной или переменных категориального типа.
Основная идея – разбиение всего пространства на прямоугольники, необязательного одинакового размера, в которых выходная переменная считается постоянной. Заметим, что существует сильная зависимость между объемом обучающей выборки и ошибкой ответа дерева.
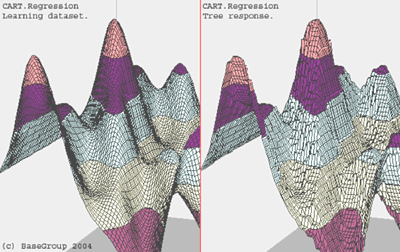
Процесс построения дерева происходит последовательно. На первом шаге мы получаем регрессионную оценку просто как константу по всему пространству примеров. Константу считаем просто как среднее арифметическое выходной переменной в обучающей выборке. Итак, если мы обозначим все значения выходной переменной как Y1, Y2, …, Yn тогда регрессионная оценка получается:
$$\widehat{f}\,(x) = \Bigl(\frac{1}{n}\sum_{i=1}^n Y_i\Bigr)\,\cdot\,I_R(x)$$
где R – пространство обучающих примеров, n – число примеров, Ir(x) – индикаторная функция пространства – фактически, набор правил, описывающих попадание переменной x в пространство. Мы рассматриваем пространство R как прямоугольник. На втором шаге мы делим пространство на две части. Выбирается некоторая переменная xi и если переменная числового типа, тогда мы определяем:
$$R_1 = \{x\,\in\,R:\,x\,\leq\,\alpha\},\,R_2 = \{x\,\in\,R:\,x\,>\,\alpha\}$$
Если xi категориального типа с возможными значениями A1, A2, …, Aq, тогда выбирается некоторое подмножество I {A1, … An} и мы определяем
$$R_1 = \{x\,\in\,R:\,x\,\in \,I\},\,R_2 = \{x\,\in\,R:\,x\,\in \,\{A_1,\,A_2,\,\dots,\,A_q\}\,\,/I\}$$
Регрессионная оценка принимает вид:
$$\widehat{f}\,(x) = \biggl(\frac{1}{|L_1|}\,\sum_{I_1}Y_i\biggr)\,\cdot\,I_{R1}(x)\,+\,\biggl(\frac{1}{|L_2|}\,\sum_{I_2}Y_i\biggr)\,\cdot\,I_{R2}(x)$$
,где I1 = {i, xi R1} и |I1| – число элементов в I1.
Каким образом выбирается лучшее разбиение? В качестве оценки здесь служит сумма квадратов разностей:
$$E = \sum_{i=1}^n {\Bigl(Y_i\,-\,\widehat{f}\,(x_i)\Bigr)}^2$$
Выбирается разбиение с минимальной суммой квадратов разностей.
Мы продолжаем разбиение до тех пор, пока в каждом подпространстве не останется малое число примеров или сумма квадратов разностей не станет меньше некоторого порога.
Отсечение, выбор финального дерева
Происходят аналогично дереву классификации. Единственное отличие – определение ошибки ответа дерева:
$$R\,(\widehat{f}) = \frac{1}{n}\sum_{i=1}^n {\Bigl(Y_i\,-\,\widehat{f}\,(x_i)\Bigr)}^2$$
,или, иначе говоря, среднеквадратичная ошибка ответа.
Стоимость дерева равна:
$$C_{\alpha}\,(\widehat{f}) = R\,(\widehat{f})\,+\,\alpha\,|\widehat{f}|$$
Остальные операции происходят аналогично дереву классификации.
Заключение
Алгоритм CART успешно сочетает в себе качество построенных моделей и, при удачной реализации, высокую скорость их построения. Включает в себя уникальные методики обработки пропущенных значений и построения оптимального дерева совокупностью алгоритмов cost-complexity pruning и V-fold cross-validation.
- L. Breiman, J.H. Friedman, R.A. Olshen, and C.T. Stone. Classification and Regression Trees. Wadsworth, Belmont, California, 1984.
- J.R. Quinlan. C4.5 Programs for Machine Learning. Morgan Kaufmann, San Mateo, California, 1993.
- Machine Learning, Neural and Statistical Classification. Editors: D. Michie, D.J. Spiegelhalter, C.C. Taylor, 02/17/1994.
- Distribution based trees are more accurate. L.Breiman, N. Shang.