Деревья решений — CART математический аппарат. Часть 1

Методология7 комментариевВерсия для печати

Общий принцип построения деревьев решений был дан в статье "Деревья решений – основные принципы работы".

В этой статье речь пойдет об алгоритме CART. CART, сокращение от Classification And Regression Tree, переводится как "Дерево Классификации и регрессии" – алгоритм бинарного дерева решений, впервые опубликованный Бриманом и др. в 1984 году [1]. Алгоритм предназначен для решения задач классификации и регрессии. Существует также несколько модифицированных версий – алгоритмы IndCART и DB-CART. Алгоритм IndCART, является частью пакета Ind и отличается от CART использованием иного способа обработки пропущенных значений, не осуществляет регрессионную часть алгоритма CART и имеет иные параметры отсечения. Алгоритм DB-CART базируется на следующей идее: вместо того чтобы использовать обучающий набор данных для определения разбиений, используем его для оценки распределения входных и выходных значений и затем используем эту оценку, чтобы определить разбиения. DB, соответственно означает – "distribution based". Утверждается, что эта идея дает значительное уменьшение ошибки классификации, по сравнению со стандартными методами построения дерева. Основными отличиями алгоритма CART от алгоритмов семейства ID3 являются:

• бинарное представление дерева решений;
• функция оценки качества разбиения;
• механизм отсечения дерева;
• алгоритм обработки пропущенных значений;
• построение деревьев регрессии.

Бинарное представление дерева решений

В алгоритме CART каждый узел дерева решений имеет двух потомков. На каждом шаге построения дерева правило, формируемое в узле, делит заданное множество примеров (обучающую выборку) на две части – часть, в которой выполняется правило (потомок – right) и часть, в которой правило не выполняется (потомок – left). Для выбора оптимального правила используется функция оценки качества разбиения.

Функция оценки качества разбиения

Обучение дерева решений относится к классу обучения с учителем, то есть обучающая и тестовая выборки содержат классифицированный набор примеров. Оценочная функция, используемая алгоритмом CART, базируется на интуитивной идее уменьшения нечистоты (неопределённости) в узле. Рассмотрим задачу с двумя классами и узлом, имеющим по 50 примеров одного класса. Узел имеет максимальную "нечистоту". Если будет найдено разбиение, которое разбивает данные на две подгруппы 40:5 примеров в одной и 10:45 в другой, то интуитивно "нечистота" уменьшится. Она полностью исчезнет, когда будет найдено разбиение, которое создаст подгруппы 50:0 и 0:50. В алгоритме CART идея "нечистоты" формализована в индексе Gini. Если набор данных Т содержит данные n классов, тогда индекс Gini определяется как:

$Gini\,(T) = 1 - \sum\limits_{i=1}^{n}\ p_i^2$ ,

где p_i – вероятность (относительная частота) класса i в T.

Если набор Т разбивается на две части Т₁ и Т₂ с числом примеров в каждом N₁ и N₂ соответственно, тогда показатель качества разбиения будет равен:

$$Gini_{split}\,(T) = \frac{N_1}{N}\,\cdot\,Gini\,(T_1)\,+\,\frac{N_2}{N}\,\cdot\,Gini\,(T_2)$$

Наилучшим считается то разбиение, для которого Gini_split(T) минимально.

Обозначим N – число примеров в узле – предке, L, R – число примеров соответственно в левом и правом потомке, l_i и r_i – число экземпляров i-го класса в левом/правом потомке. Тогда качество разбиения оценивается по следующей формуле:

$$Gini_{split}\, = \frac{L}{N}\,\cdot\,\Biggl(1\,-\,\sum_{i=1}^n\,{\biggl(\frac{l_i}{L}\biggr)}^2\Biggr)\,+\,\frac{R}{N}\,\cdot\,\Biggl(1\,-\,\sum_{i=1}^n\,{\biggl(\frac{r_i}{R}\biggr)}^2\Biggr)\,\rightarrow\,\min$$

Чтобы уменьшить объем вычислений формулу можно преобразовать:

$$Gini_{split}\, = \frac{1}{N}\Biggl(L\,\cdot\,\biggl(1\,-\,\frac{1}{L^2}\,\cdot\,\sum_{i=1}^n l_i^2 \biggr)\,+\,R\,\cdot\,\biggl(1\,-\,\frac{1}{R^2}\,\cdot\,\sum_{i=1}^n r_i^2\biggr)\Biggr)\rightarrow\min$$

Так как умножение на константу не играет роли при минимизации:

$$Gini_{split}\, =L\,-\,\frac{1}{L}\,\cdot\,\sum_{i=1}^n l_i^2 \,+\,R\,-\,\frac{1}{R}\,\cdot\,\sum_{i=1}^n r_i^2\rightarrow\min$$

$$Gini_{split}\, =N\,-\,\biggl(\frac{1}{L}\,\cdot\,\sum_{i=1}^n l_i^2 \,+\,\frac{1}{R}\,\cdot\,\sum_{i=1}^n r_i^2\biggr)\rightarrow\min$$

$$\widetilde{G}_{split}\, =\frac{1}{L}\,\cdot\,\sum_{i=1}^n l_i^2 \,+\,\frac{1}{R}\,\cdot\,\sum_{i=1}^n r_i^2\rightarrow\max$$

В итоге, лучшим будет то разбиение, для которого величина максимальна. Реже в алгоритме CART используются другие критерии разбиения Twoing, Symmetric Gini и др., подробнее см. [1].

Правила разбиения

Вектор предикторных переменных, подаваемый на вход дерева может содержать как числовые (порядковые) так и категориальные переменные. В любом случае в каждом узле разбиение идет только по одной переменной. Если переменная числового типа, то в узле формируется правило вида x_i <= c. Где с – некоторый порог, который чаще всего выбирается как среднее арифметическое двух соседних упорядоченных значений переменной x_i обучающей выборки. Если переменная категориального типа, то в узле формируется правило x_i V(x_i), где V(x_i) – некоторое непустое подмножество множества значений переменной x_i в обучающей выборке. Следовательно, для n значений числового атрибута алгоритм сравнивает n-1 разбиений, а для категориального (2^n-1 – 1). На каждом шаге построения дерева алгоритм последовательно сравнивает все возможные разбиения для всех атрибутов и выбирает наилучший атрибут и наилучшее разбиение для него.

Механизм отсечения дерева

Механизм отсечения дерева, оригинальное название minimal cost-complexity tree pruning, – наиболее серьезное отличие алгоритма CART от других алгоритмов построения дерева. CART рассматривает отсечение как получение компромисса между двумя проблемами: получение дерева оптимального размера и получение точной оценки вероятности ошибочной классификации.

Основная проблема отсечения – большое количество всех возможных отсеченных поддеревьев для одного дерева. Более точно, если бинарное дерево имеет |T| – листов, тогда существует ~[1.5028369^|T|] отсечённых поддеревьев. И если дерево имеет хотя бы 1000 листов, тогда число отсечённых поддеревьев становится просто огромным.

Базовая идея метода – не рассматривать все возможные поддеревья, ограничившись только "лучшими представителями" согласно приведённой ниже оценке.

Обозначим |T| – число листов дерева, R(T) – ошибка классификации дерева, равная отношению числа неправильно классифицированных примеров к числу примеров в обучающей выборке. Определим $C_{\alpha}\,(T)$ – полную стоимость (оценку/показатель затраты-сложность) дерева Т как:

$C_{\alpha}\,(T) = R\,(T)\,+\,\alpha\,*\,|T|$, где |T| – число листов (терминальных узлов) дерева, – некоторый параметр, изменяющийся от 0 до + $\infty$. Полная стоимость дерева состоит из двух компонент – ошибки классификации дерева и штрафа за его сложность. Если ошибка классификации дерева неизменна, тогда с увеличением полная стоимость дерева будет увеличиваться. Тогда в зависимости от менее ветвистое дерево, дающее бОльшую ошибку классификации может стоить меньше, чем дающее меньшую ошибку, но более ветвистое.

Определим T_max – максимальное по размеру дерево, которое предстоит обрезать. Если мы зафиксируем значение $\alpha$, тогда существует наименьшее минимизируемое поддерево $\alpha$, которое выполняет следующие условия:

1. $C_{\alpha}\Bigl(T\,(\alpha)\Bigr) = min_{\,\,T \leq T_{\max}}\,C_{\alpha}(T)$
2. $if\,\,C_{\alpha}\,(T) = C_{\alpha}\Bigl(T\,(\alpha)\Bigr)\,then\,\,T\,(\alpha)\leq\,T$

Первое условие говорит, что не существует такого поддерева дерева T_max , которое имело бы меньшую стоимость, чем $T\,(\alpha)$ при этом значении $\alpha$. Второе условие говорит, что если существует более одного поддерева, имеющего данную полную стоимость, тогда мы выбираем наименьшее дерево.

Можно показать, что для любого значения существует такое наименьшее минимизируемое поддерево. Но эта задача не тривиальна. Что она говорит – что не может быть такого, когда два дерева достигают минимума полной стоимости и они несравнимы, т.е. ни одно из них не является поддеревом другого. Мы не будем доказывать этот результат.

Хотя имеет бесконечное число значений, существует конечное число поддеревьев дерева Tmax. Можно построить последовательность уменьшающихся поддеревьев дерева T_max:

T₁ > T₂ > T₃ >...> {t₁},

(где t₁ – корневой узел дерева) такую, что T_k – наименьшее минимизируемое поддерево для $[\alpha_k,\,\alpha_{k+1})$. Это важный результат, так как это означает, что мы можем получить следующее дерево в последовательности, применив отсечение к текущему дереву. Это позволяет разработать эффективный алгоритм поиска наименьшего минимизируемого поддерева при различных значениях $\alpha$. Первое дерево в этой последовательности – наименьшее поддерево дерева T_max имеющее такую же ошибку классификации, как и T_max, т.е. $T_1 = T(\alpha=0)$. Пояснение: если разбиение идет до тех пор, пока в каждом узле останется только один класс, то T₁ = T_max, но так как часто применяются методы ранней остановки (prepruning), тогда может существовать поддерево дерева T_max имеющее такую же ошибку классификации.

Вклад T_t в полную стоимость дерева Т составит $C_{\alpha}(T_t) = R\,(T_t)\,+\,\alpha\,|T_t|$, где

$R\,(T_t) = \sum_{{t'}\in {T_t}}{R(t')}$

Дерево T – T_t будет лучше, чем Т, когда $C_{\alpha}\{(t\}) = C_{\alpha}\,(T_t)$, потому что при этой величине они имеют одинаковую стоимость, но T – T_t наименьшее из двух. Когда $C_{\alpha}\{(t\}) = C_{\alpha}\,(T_t)$ мы получаем:

$$R\,(T_t)\,+\,\alpha\,|T_t| = R\,(t)\,+\,\alpha$$

решая для $\alpha$, получаем:

$$\alpha = \frac{R\,(t)\,-\,R\,(T_t)}{|T_t|\,-\,1}$$

Так для любого узла t в Т₁ ,если мы увеличиваем $\alpha$, тогда когда

$$\alpha = \frac{R\,(t)\,-\,R\,(T_{1,\,t})}{|T_{1,\,t}|\,-\,1}$$

дерево, полученное отсечением в узле t, будет лучше, чем Т₁.

Основная идея состоит в следующем: вычислим это значение для каждого узла в дереве Т₁, и затем выберем "слабые связи" (их может быть больше чем одна), т.е. узлы для которых величина

$$g\,(t) = \frac{R\,(t)\,-\,R\,(T_{1,\,t})}{|T_{1,\,t}|\,-\,1}$$

является наименьшей. Мы отсекаем Т₁ в этих узлах, чтобы получить Т₂ – следующее дерево в последовательности. Затем мы продолжаем этот процесс для полученного дерева и так пока мы не получим корневой узел (дерево в котором только один узел).

Рассмотрим метод подробнее на примере.

В качестве примера вычислим последовательность поддеревьев и соответствующих значений для дерева изображенного на рис. 1.

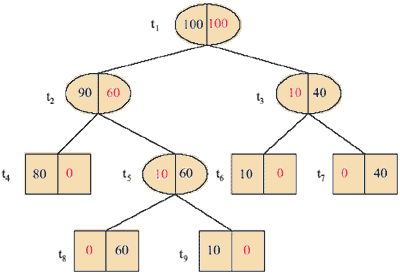
Очевидно, что Т₁ = Т_max , так как все листы содержат примеры одного класса и отсечение любого узла (t₃ или t₅) приведёт к возрастанию ошибки классификации.
Затем мы вычисляем g₁(t) для всех узлов t в Т₁.

$$g\,(t_1) = \frac{R\,(t_1)\,-\,R\,(T_{1,\,t_1})}{|T_{1,\,t_1}|\,-\,1}$$

R(t₁) – ошибка классификации. Если превратить t₁ в лист, то следует сопоставить ему какой либо класс; так как число примеров обоих классов одинаково (равно 100), то класс выбираем наугад, в любом случае он неправильно классифицирует 100 примеров. Всего дерево обучалось на 200 примеров (100+100=200 для корневого узла). R(t₁) = m/n. m=100, n=200. R(t₁) = 1/2.

$R\,(T_1,\,t_1)$– сумма ошибок всех листов поддерева. Считается как сумма по всем листам отношений количества неправильно классифицированных примеров в листе к общему числу примеров для дерева. В примере все делим на 200. Так как для поддерева с корнем в t₁ оно же дерево Т₁ все листы не имеют неправильно классифицированных примеров, поэтому

$$R\,(T_1,\,t_1) = \sum_1^5\frac{0}{200} = 0$$

$|T_1,\,t_1|$ количество листов поддерева с корнем в узле t₁. Итого их – 5.

Получаем:

g₁(t₁) = (1/2 – 0)/(5 – 1) = 1/8.
g₁(t₂) = 3/20.
g₁(t₃) = 1/20.
g₁(t₅) = 1/20.

Узлы t₃ и t₅ оба хранят минимальное значение g₁, мы получаем новое дерево Т₂, обрезая Т₁ в обоих этих узлах. Мы получили дерево изображенное на рис.2.

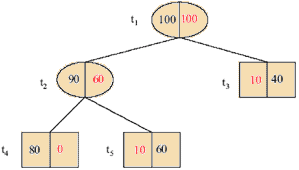
Далее мы продолжаем вычислять g-значение для Т₂.

g₂(t₁) = (100/200 – (0/200 + 10/200 + 10/200)) / (3 – 1) = 2/10.

g₂(t₂) = (60/200 – (0/200 + 10/200)) / (2 – 1) = 1/4.

Минимум хранится в узле t₁, поэтому мы обрезаемы в t₁ и получаем корень дерева (T₃ = {t₁}). На этом процесс отсечения заканчивается.

Последовательность значений получается: $\alpha$₁ = 0, $\alpha$₂ = 1/20, $\alpha$₃ = 2/10. Итак, Т₁ является лучшим деревом для [0, 1/20), T₂ – для [1/20, 2/10) и Т₃ = {t₁} для [2/10, $\infty$).

Выбор финального дерева

Итак, мы имеем последовательность деревьев, нам необходимо выбрать лучшее дерево из неё. То, которое мы и будем использовать в дальнейшем. Наиболее очевидным является выбор финального дерева через тестирование на тестовой выборке. Дерево, давшее минимальную ошибку классификации, и будет лучшим. Однако, это не единственно возможный путь.

Продолжение описания см. в статье "Описание алгоритма CART. Часть 2".