Калмановская фильтрация

Очистка данных, Предобработка данных55 комментариевВерсия для печати

Введение

Винеровские фильтры лучше всего подходят для обработки процессов или отрезков процессов в целом (блочная обработка). Для последовательной обработки требуется текущая оценка сигнала на каждом такте с учетом информации, поступающей на вход фильтра в процессе наблюдения.

При винеровской фильтрации каждый новый отсчет сигнала потребовал бы пересчета всех весовых коэффициентов фильтра. В настоящее время широкое распространение получили адаптивные фильтры, в которых поступающая новая информация используется для непрерывной корректировки ранее сделанной оценки сигнала (сопровождение цели в радиолокации, системы автоматического регулирования в управлении и т.д). Особенный интерес представляют адаптивные фильтры рекурсивного типа, известные как фильтр Калмана.

Эти фильтры широко используются в контурах управления в системах автоматического регулирования и управления. Именно оттуда они и появились, подтверждением чему служит столь специфическая терминология, используемая при описании их работы, как пространство состояний.

Одна из основных задач, требующих своего решения в практике нейронных вычислений, – получение быстрых и надежных алгоритмов обучения НС. В этой связи может оказаться полезным использование в контуре обратной связи обучающего алгоритма линейных фильтров. Так как обучающие алгоритмы имеют итеративную природу, такой фильтр должен представлять собой последовательное рекурсивное устройство оценки.

Задача оценки параметров

Одной из задач теории статистических решений, имеющих большое практическое значение, является задача оценки векторов состояния и параметров систем, которая формулируется следующим образом. Предположим, необходимо оценить значение векторного параметра $X$, недоступного непосредственному измерению. Вместо этого измеряется другой параметр $Z$, зависящий от $X$. Задача оценивания состоит в ответе на вопрос: что можно сказать об $X$, зная $Z$. В общем случае, процедура оптимальной оценки вектора $X$ зависит от принятого критерия качества оценки.

Например, байесовский подход к задаче оценки параметров требует полной априорной информации о вероятностных свойствах оцениваемого параметра, что зачастую невозможно. В этих случаях прибегают к методу наименьших квадратов (МНК), который требует значительно меньше априорной информации.

Рассмотрим применения МНК для случая, когда вектор наблюдения $Z$ связан с вектором оценки параметров $X$ линейной моделью, и в наблюдении присутствует помеха $V$, некоррелированная с оцениваемым параметром:

$Z = HX + V$, (1)

где $H$ – матрица преобразования, описывающая связь наблюдаемых величин с оцениваемыми параметрами.

Оценка $X$, минимизирующая квадрат ошибки, записывается следующим образом:

$X_{оц}=(H^TR_V^{-1}H)^{-1}H^TR_V^{-1}Z$, (2)

Пусть помеха $V$ не коррелирована, в этом случае матрица $R_V$ есть просто единичная матрица, и уравнение для оценки становится проще:

$X_{оц}=(H^TH)^{-1}H^TZ$, (3)

Запись в матричной форме сильно экономит бумагу, но может быть для кого то непривычна. Следующий пример, взятый из монографии Коршунова Ю. М. "Математические основы кибернетики", все это иллюстрирует.
Имеется следующая электрическая цепь:

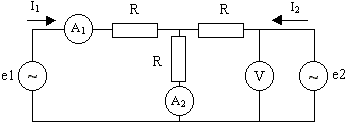
Наблюдаемые величины в данном случае – показания приборов $A_1 = 1 A, A_2 = 2 A, V = 20 B$.

Кроме того, известно сопротивление $R = 5$ Ом. Требуется оценить наилучшим образом, с точки зрения критерия минимума среднего квадрата ошибки значения токов $I_1$ и $I_2$. Самое важное здесь заключается в том, что между наблюдаемыми величинами (показаниями приборов) и оцениваемыми параметрами существует некоторая связь. И эта информация привносится извне.

В данном случае, это законы Кирхгофа, в случае фильтрации (о чем речь пойдет дальше) – авторегрессионная модель временного ряда, предполагающая зависимость текущего значения от предшествующих.

Итак, знание законов Кирхгофа, никак не связанное с теорией статистических решений, позволяет установить связь между наблюдаемыми значениями и оцениваемыми параметрами (кто изучал электротехнику – могут проверить, остальным придется поверить на слово):

$$z_1 = A_1 = I_1 + \xi_1 = 1$$

$$z_2 = A_2 = I_1 + I_2 + \xi_2 = 2$$

$$z_2 = V/R = I_1 + 2 * I_2 + \xi_3 = 4$$

Это же в векторной форме:

$$\begin{vmatrix} z_1\\ z_2\\ z_3 \end{vmatrix} = \begin{vmatrix} 1 & 0\\ 1 & 1\\ 1 & 2 \end{vmatrix} \begin{vmatrix} I_1\\ I_2 \end{vmatrix} + \begin{vmatrix} \xi_1\\ \xi_2\\ \xi_3 \end{vmatrix}$$

Или $Z = HX + V$, где

$$Z= \begin{vmatrix} z_1\\ z_2\\ z_3 \end{vmatrix} = \begin{vmatrix} 1\\ 2\\ 4 \end{vmatrix} ; H= \begin{vmatrix} 1 & 0\\ 1 & 1\\ 1 & 2 \end{vmatrix} ; X= \begin{vmatrix} I_1\\ I_2 \end{vmatrix} ; V= \begin{vmatrix} \xi_1\\ \xi_2\\ \xi_3 \end{vmatrix}$$

Считая значения помехи некоррелированными между собой, найдем оценку I₁ и I₂ по методу наименьших квадратов в соответствии с формулой 3:

$H^TH= \begin{vmatrix} 1 & 1& 1\\ 0 & 1& 2 \end{vmatrix} \begin{vmatrix} 1 & 0\\ 1 & 1\\ 1 & 2 \end{vmatrix} = \begin{vmatrix} 3 & 3\\ 3 & 5 \end{vmatrix} ; (H^TH)^{-1}= \frac{1}{6} \begin{vmatrix} 5 & -3\\ -3 & 3 \end{vmatrix} $;

$H^TZ= \begin{vmatrix} 1 & 1& 1\\ 0 & 1& 2 \end{vmatrix} \begin{vmatrix} 1 \\ 2\\ 4 \end{vmatrix} = \begin{vmatrix} 7\\ 10 \end{vmatrix} ; X{оц}= \frac{1}{6} \begin{vmatrix} 5 & -3\\ -3 & 3 \end{vmatrix} \begin{vmatrix} 7\\ 10 \end{vmatrix} = \frac{1}{6} \begin{vmatrix} 5\\ 9 \end{vmatrix}$;

Итак $I_1 = 5/6 = 0,833 A$; $I_2 = 9/6 = 1,5 A$.

Задача фильтрации

В отличие от задачи оценки параметров, которые имеют фиксированные значения, в задаче фильтрации требуется оценивать процессы, то есть находить текущие оценки изменяющегося во времени сигнала, искаженного помехой, и, в силу этого, недоступного непосредственному измерению. В общем случае вид алгоритмов фильтрации зависит от статистических свойств сигнала и помехи.

Будем предполагать, что полезный сигнал – медленно меняющаяся функция времени, а помеха – некоррелированный шум. Будем использовать метод наименьших квадратов, опять же по причине отсутствия априорных сведений о вероятностных характеристиках сигнала и помехи.

Вначале получим оценку текущего значения $x_n$ по имеющимся $k$ последним значениям временного ряда $z_n, z_{n-1},z_{n-2}\dots z_{n-(k-1)}$. Модель наблюдения та же, что и в задаче оценки параметров:

$$Z = HX + V$$

Понятно, что $Z$ – это вектор–столбец, состоящий из наблюдаемых значений временного ряда $z_n, z_{n-1},z_{n-2}\dots z_{n-(k-1)}$, $V$ – вектор–столбец помехи $\xi _n, \xi _{n-1},\xi_{n-2}\dots \xi_{n-(k-1)}$, искажающий истинный сигнал. А что означают символы $H$ и $X$? О каком, например, векторе–столбце $X$ может идти речь, если все, что необходимо, – это дать оценку текущего значения временного ряда? А что понимать под матрицей преобразований $H$, вообще непонятно.

На все эти вопросы можно ответить только при условии введения в рассмотрение понятия модели генерации сигнала. То есть, необходима некоторая модель исходного сигнала. Это и понятно, при отсутствии априорной информации о вероятностных характеристиках сигнала и помехи остается только строить предположения. Можно назвать это гаданием на кофейной гуще, но специалисты предпочитают другую терминологию. На их "фене" это называется параметрическая модель.

В данном случае оцениваются параметры именно этой модели. При выборе подходящей модели генерации сигнала вспомним о том, что любую аналитическую функцию можно разложить в ряд Тейлора. Поразительное свойство ряда Тейлора заключается в том, что форма функции на любом конечном расстоянии $t$ от некой точки $x=a$ однозначно определяется поведением функции в бесконечно малой окрестности точки $x=a$ (речь идет о ее производных первого и высшего порядков).

Таким образом, существование рядов Тейлора означает, что аналитическая функция обладает внутренней структурой с очень сильной связью. Если, например, ограничиться тремя членами ряда Тейлора, то модель генерации сигнала будет выглядеть так:

$x_{n-i} = F_{-i}x_n$, (4)

где:

$$X_n= \begin{vmatrix} x_n\\ x'_n\\ x''_n \end{vmatrix} ; F_{-i}= \begin{vmatrix} 1 & -i & i^2/2\\ 0 & 1 & -i\\ 0 & 0 & 1 \end{vmatrix} $$

То есть формула 4, при заданном порядке полинома (в примере он равен 2) устанавливает связь между $n$-ым значением сигнала во временной последовательности и $(n-i)$–ым. Таким образом, оцениваемый вектор состояния в данном случае включает в себя, помимо собственно оцениваемого значения, первую и вторую производную сигнала.

В теории автоматического управления такой фильтр назвали бы фильтром с астатизмом 2-го порядка. Матрица преобразования $H$ для данного случая (оценка осуществляется по текущему и $k-1$ предшествующим выборкам) выглядит так:

$$H= \begin{vmatrix} 1 & -k & k^2/2\\ - & - & -\\ 1 & -2 & 2\\ 1 & -1 & 0.5\\ 1 & 0 & 0 \end{vmatrix}$$

Все эти числа получаются из ряда Тейлора в предположении, что временной интервал между соседними наблюдаемыми значениями постоянный и равен 1.

Итак, задача фильтрации при принятых нами предположениях свелась к задаче оценки параметров; в данном случае оцениваются параметры принятой нами модели генерации сигнала. И оценка значений вектора состояния $X$ осуществляется по той же формуле 3:

$$X_{оц}=(H^TH)^{-1}H^TZ$$

По сути, мы реализовали процесс параметрического оценивания, основанный на авторегрессионной модели процесса генерации сигнала.

Формула 3 легко реализуется программно, для этого нужно заполнить матрицу $H$ и вектор столбец наблюдений $Z$. Такие фильтры называются фильтры с конечной памятью, так как для получения текущей оценки $X_{nоц}$ они используют последние $k$ наблюдений. На каждом новом такте наблюдения к текущей совокупности наблюдений прибавляется новое и отбрасывается старое. Такой процесс получения оценок получил название скользящего окна.

Фильтры с растущей памятью

Фильтры с конечной памятью обладают тем основным недостатком, что после каждого нового наблюдения необходимо заново производить полный пересчет по всем хранящимся в памяти данным. Кроме того, вычисление оценок можно начинать только после того, как накоплены результаты первых $k$ наблюдений. То есть эти фильтры обладают большой длительностью переходного процесса.

Чтобы бороться с этим недостатком, необходимо перейти от фильтра с постоянной памятью к фильтру с растущей памятью. В таком фильтре число наблюдаемых значений, по которым производится оценка, должна совпадать с номером n текущего наблюдения. Это позволяет получать оценки, начиная с числа наблюдений, равного числу компонент оцениваемого вектора $X$. А это определяется порядком принятой модели, то есть сколько членов из ряда Тейлора используется в модели.

При этом с ростом n улучшаются сглаживающие свойства фильтра, то есть повышается точность оценок. Однако непосредственная реализация этого подхода связана с возрастанием вычислительных затрат. Поэтому фильтры с растущей памятью реализуются как рекуррентные.

Дело в том, что к моменту n мы уже имеем оценку $X_{(n-1)оц}$, в которой содержится информация обо всех предыдущих наблюдениях $z_n, z_{n-1}, z_{n-2} \dots z_{n-(k-1)}$. Оценку $X_{nоц}$ получаем по очередному наблюдению $z_n$ с использованием информации, хранящейся в оценке $X_{(n-1)}{\mbox {оц}}$. Такая процедура получила название рекуррентной фильтрации и состоит в следующем:

• по оценке $X_{(n-1)}{\mbox {оц}}$ прогнозируют оценку $X_n$ по формуле 4 при $i = 1$: $X_{\mbox {nоцаприори}} = F_1X_{(n-1)оц}$. Это априорная оценка;
• по результатам текущего наблюдения $z_n$, эту априорную оценку превращают в истинную, то есть апостериорную;
• эта процедура повторяется на каждом шаге, начиная с $r+1$, где $r$ – порядок фильтра.

Окончательная формула рекуррентной фильтрации выглядит так:

$X_{(n-1)оц} = X_{\mbox {nоцаприори}} + (H^T_nH_n)^{-1}h^T_0(z_n - h_0 X_{\mbox {nоцаприори}})$, (6)

где для нашего фильтра второго порядка:

$$$$

Фильтр с растущей памятью, работающий в соответствии с формулой 6 – частный случай алгоритма фильтрации, известного под названием фильтра Калмана.

При практической реализации этой формулы необходимо помнить, что входящая в него априорная оценка определяется по формуле 4, а величина $h_0 X_{\mbox {nоцаприори}}$ представляет собой первую компоненту вектора $X_{\mbox {nоцаприори}}$.

У фильтра с растущей памятью имеется одна важная особенность. Если посмотреть на формулу 6, то окончательная оценка есть сумма прогнозируемого вектора оценки и корректирующего члена. Эта поправка велика при малых $n$ и уменьшается при увеличении $n$, стремясь к нулю при $n \rightarrow \infty$. То есть с ростом n сглаживающие свойства фильтра растут и начинает доминировать модель, заложенная в нем. Но реальный сигнал может соответствовать модели лишь на отдельных участках, поэтому точность прогноза ухудшается.

Чтобы с этим бороться, начиная с некоторого $n$, накладывают запрет на дальнейшее уменьшение поправочного члена. Это эквивалентно изменению полосы фильтра, то есть при малых n фильтр более широкополосен (менее инерционен), при больших – он становится более инерционен.

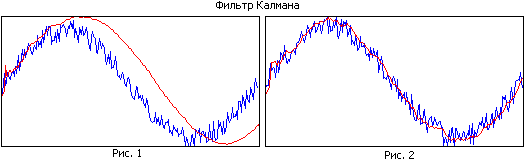
Сравните рисунок 1 и рисунок 2. На первом рисунке фильтр имеет большую память, при этом он хорошо сглаживает, но в силу узкополосности оцениваемая траектория отстает от реальной. На втором рисунке память фильтра меньше, он хуже сглаживает, но лучше отслеживает реальную траекторию.