Применение логистической регрессии в медицине и скоринге
Введение
В предыдущей статье цикла был рассмотрен математический аппарат логистической регрессии и ROC-анализа. Этот материал посвещен практическим аспектам применения данных инструментов. Рассмотрим более подробно на двух областях – диагностика заболеваний и оценка кредитоспособности физлиц.
Пример из медицины
Первый пример, на котором мы остановимся, будет диагностика диабета (набор данных взят из UCI machine learning repository). Обучающая выборка содержит 768 записей со следующими полями:
- Число случаев беременности;
- Концентрация глюкозы;
- Артериальное диастолическое давление, мм. рт. ст.;
- Толщина кожной складки трехглавой мышцы, мм.;
- 2-х часовой сывороточный инсулин;
- Индекс массы тела;
- Числовой параметр наследственности диабета;
- Возраст, лет;
- Зависимая переменная (1 – наличие заболевания, 0 – отсутствие).
Распределение зависимой переменной следующее: 500 случаев отсутствия заболевания, 268 – его наличие.
Рассчитанные коэффициенты логистической регрессии приведены в таблице.
| Независимая переменная | Коэффициент |
|---|---|
| 1 | 0.1232 |
| 2 | 0.0352 |
| 3 | -0.0133 |
| 4 | 0.0006 |
| 5 | -0.0012 |
| 6 | 0.0897 |
| 7 | 0.9452 |
| 8 | 0.0149 |
| Константа | -8.4047 |
Значение логарифмического правдоподобия -2*Likehood равно 723.45. На рис. 1 изображена ROC-кривая. Предсказательную способность модели можно охарактеризовать как очень хорошую.
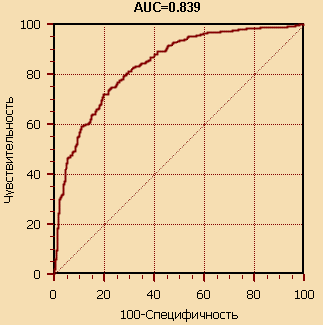
Рассмотрим фрагмент массива точек "Чувствительность-Специфичность".
| Порог | Se, % | Sp, % | Se+Sp | |Se-Sp| |
|---|---|---|---|---|
... |
... |
... |
... |
... |
0.25 |
84.3 |
65.0 |
149.3 |
19.3 |
0.26 |
83.6 |
65.6 |
149.2 |
18.0 |
0.27 |
83.2 |
67.4 |
150.6 |
15.8 |
... |
... |
... |
... |
... |
0.31 |
78.0 |
73.0 |
151.0 |
5.0 |
0.32 |
76.1 |
75.0 |
151.1 |
1.1 |
0.33 |
75.4 |
75.6 |
151.0 |
0.2 |
0.34 |
75.0 |
76.8 |
151.8 |
1.8 |
0.35 |
74.3 |
77.8 |
152.1 |
3.5 |
0.36 |
72.0 |
79.2 |
151.2 |
7.2 |
0.37 |
70.9 |
80.2 |
151.1 |
9.3 |
0.38 |
69.4 |
80.8 |
150.2 |
11.4 |
0.39 |
69.3 |
81.2 |
150.5 |
11.9 |
0.40 |
67.2 |
82.0 |
149.2 |
14.8 |
... |
... |
... |
... |
... |
0.49 |
58.6 |
88.8 |
147.4 |
30.2 |
0.50 |
58.2 |
89.0 |
147.2 |
30.8 |
0.51 |
57.8 |
89.2 |
147.0 |
31.4 |
... |
... |
... |
... |
... |
Как следует из таблицы, оптимальным порогом классификации, обеспечивающим максимум чувствительности и специфичности теста (или минимум ошибок I и II рода), является точка 0.35. В ней чувствительность равна 74.3%, что означает: у 74.3% пациентов с наличием диабета диагностический тест будет положителен. Специфичность равна 77.8%, следовательно, у 77.8% пациентов, у которых нет диабета, результаты теста отрицательны.
Точкой баланса, в которой чувствительность и специфичность примерно совпадают, является 0.33.
Если мы, например, выберем порог 0.25, в котором чувствительность теста очень высокая (>84%), то получим гипердиагностику пациентов. А если зафиксировать порог на уровне 0.5, то будем диагностировать только доподлинно больных (специфичность 89%). Что считать здесь оптимальным порогом? Все зависит от конкретной задачи, универсальных рецептов нет. В диагностике диабета, наверное, следует выбрать наиболее чувствительный тест: ложноположительный результат может угрожать, например, лишь дополнительным визитом к врачу, а ложноотрицательный – не выявлением опасной, но излечимой болезни.
Пример из скоринга
Технологии скоринга – автоматической оценке кредитоспособности физического лица – сегодня уделяется повышенное внимание. Логистическая регрессия является традиционным статистическим инструментом для расчета коэффициентов (баллов) скоринговой карты на основе накопленной кредитной истории. А ROC-анализ обеспечивает управление рисками в зависимости от кредитной политики и стратегии организации.
Поставим модели задачу выявления неблагонадежных потенциальных заемщиков. Но, поскольку в скоринге общепринято, что чем выше рейтинг клиента, тем выше его кредитоспособность, то будем считать положительным исходом успешное погашение займа, а отрицательным – дефолт по кредиту.
Тогда проецируя при этих условиях определения чувствительности и специфичности на скоринг, можно заключить, что скоринговая модель с высокой специфичностью соответствует консервативной кредитной политике (чаще происходит отказ в выдаче кредита), а с высокой чувствительностью – политике рискованных кредитов. В первом случае минимизируется кредитный риск, связанный с потерями ссуды и процентов и дополнительными расходами на возвращение кредита, а во втором – коммерческий риск, связанный с упущенной выгодой.
Рассмотрим пример: дана обучающая выборка – производная от кредитной истории заемщиков физических лиц. По результатам характера и результата погашений все заемщики разделены на два класса: благонадежный и неблагонадежный (зависимая переменная). Независимыми переменными являются анкетные данные заемщиков:
- Возраст;
- Пол;
- Семейное остоит в браке (да/нет);
- Количество иждивенцев;
- Подтвержденный совокупный располагаемый доход;
- Опыт работы, лет;
- Срок проживания в регионе, лет;
- Рыночная стоимость недвижимости в собственности, тыс.долл.;
- Ежемесячный платеж по кредиту, руб.;
- Зависимая переменная (1 – благонадежный, 0 – неблагонадежный заемщик).
Распределение зависимой переменной следующее: 492 благонадежных заемщика из 999.
Рассчитанные коэффициенты логистической регрессии приведены в таблице.
| Независимая переменная | Коэффициент |
|---|---|
| 1 | -0.0260 |
| 2 | 0.6694 |
| 3 | -0.2408 |
| 4 | -1.8741 |
| 5 | 0.0007 |
| 6 | 0.0033 |
| 7 | 0.0094 |
| 8 | 0.0109 |
| Константа | -3.5276 |
На рис. 2 изображена ROC-кривая для этой скоринг-модели.
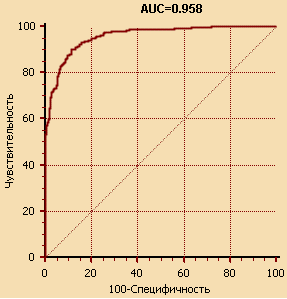
Снова рассмотрим фрагмент массива точек "Чувствительность-Специфичность".
| Порог | Se, % | Sp, % | Se+Sp | |Se-Sp| |
|---|---|---|---|---|
... |
... |
... |
... |
... |
0.40 |
91.3 |
86.6 |
177.9 |
4.7 |
0.41 |
91.1 |
86.8 |
177.9 |
4.7 |
0.42 |
90.4 |
87.0 |
177.4 |
3.4 |
0.43 |
90.4 |
88.2 |
178.6 |
2.2 |
0.44 |
89.8 |
88.4 |
178.2 |
1.4 |
0.45 |
88.6 |
88.6 |
177.2 |
0.0 |
0.46 |
88.0 |
89.0 |
177.0 |
1.0 |
0.47 |
88.0 |
89.3 |
177.3 |
1.3 |
0.48 |
87.6 |
89.5 |
177.1 |
1.9 |
0.49 |
87.6 |
90.1 |
177.7 |
2.5 |
0.50 |
87.0 |
90.3 |
177.3 |
3.3 |
0.51 |
86.2 |
90.5 |
176.7 |
4.3 |
0.52 |
85.8 |
90.7 |
176.5 |
4.9 |
0.53 |
85.6 |
90.9 |
176.5 |
5.3 |
0.54 |
85.4 |
91.1 |
176.5 |
5.7 |
... |
... |
... |
... |
... |
0.64 |
80.5 |
93.7 |
174.2 |
13.2 |
0.65 |
79.9 |
94.1 |
174.0 |
14.2 |
0.66 |
78.9 |
94.1 |
173.0 |
15.2 |
... |
... |
... |
... |
... |
Максимум чувствительности и специфичности достигается в точке 0.43. В ней чувствительность равна 90.4%, что означает, что 90.4% благонадежных заемщика будут выявлены классификатором. Специфичность равна 88.2%, следовательно, 11.8% недобросовестных заемщиков получат одобрение в выдаче кредита (кредитный риск).
Баланс между чувствительностью и специфичностью получается в точке 0.45.
Если же в банке выбрана стратегия строгого отбора заемщиков, направленная на максимальное выявление неблагонадежных клиентов, следует отдать предпочтение более высокому порогу, который соответствует высокой специфичности, например, точке 0.65 (Sp>94%). Таким образом, при помощи логистической регрессии ROC-анализа осуществляется управление рисками в кредитовании, хотя ROC-анализ может быть применен к любой модели, в которой есть выходное непрерывное поле.
Данные, использованные в материале:
- Fawcett T. ROC Graphs: Notes and Practical Considerations for Researchers // 2004 Kluwer Academic Publishers.
- Zweig M.H., Campbell G. ROC Plots: A Fundamental Evaluation Tool in Clinical Medicine // Clinical Chemistry, Vol. 39, No. 4, 1993.
- Davis J., Goadrich M. The Relationship Between Precision-Recall and ROC Curves // Proc. Of 23 International Conference on Machine Learning, Pittsburgh, PA, 2006.