Область применения
Страховые запасы предназначены для непрерывного удовлетворения спроса на заданном интервале времени. Оптимальный размер страхового запаса позволит сократить издержки на его хранение, удовлетворяя при этом заданный уровень спроса.
Описание
Классическая модель расходования и пополнения запасов является идеальной при полностью детерминированных параметрах управления запасами. На практике же приходится учитывать неопределенности, вызванные главным образом случайным характером ежедневного спроса $d_j$ и продолжительностью логистического цикла $T_i$. Случайность основных параметров поставок и спроса, а также логистические риски являются причинами создания страховых запасов.
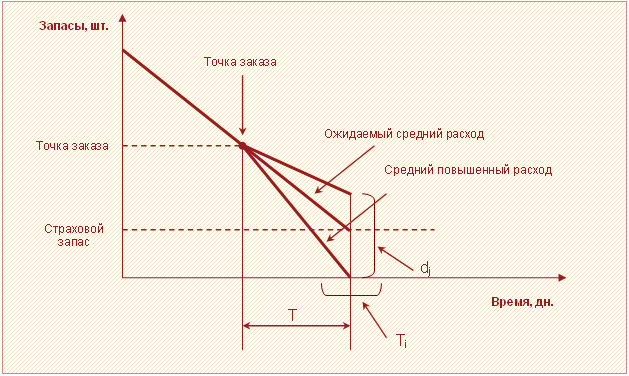
Для расчета величины страхового запаса в условиях неопределенности используют формулу Бауэрсокса:
$Q_{stk}=k \times \sigma_c$,
где
$k$ — коэффициент, определяемый с помощью табулированной функции $f(k)$,
$\sigma_c$ — общее среднее квадратичное отклонение.
Функция $f(k)$ – функция потерь, которая определяется площадью, ограниченной правой ветвью "кривой нормального распределения". Функция $f(k)$ рассчитывается по формуле:
$f(k) = \frac{(1-S_L)\times Q}{\sigma _c}$,
где
$S_L$ — величина дефицита,
$Q$ — размер заказа.
Величина дефицита $S_L$ называется также "уровнем доступности продуктов" или "желательным уровнем обслуживания". Судя по размерности, $S_L$ может быть названа вероятностью отсутствия дефицита (значение лежит в диапазоне от 0 до 1). Общее среднее квадратическое отклонение рассчитывается по формуле:
$\sigma_c = \sqrt{\bar{T}\times \sigma^2 + \bar{D}^2 \times \sigma^2_T}$,
где
$\bar{T},\bar{D}$ — соответственно среднее значение продолжительности функционального цикла и количество продаж продукта в день,
$\sigma^2_T,\sigma^2_D$ — соответственно средние квадратические отклонения случайных величин $T$ и $D$.
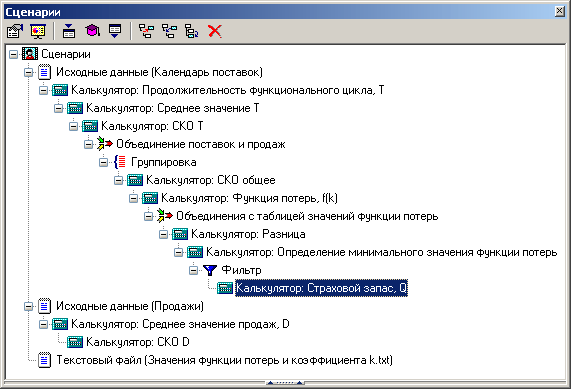
Алгоритм
- Рассчитать продолжительность, среднее и среднее квадратическое отклонение значения функционального периода.
- Рассчитать продолжительность, среднее и среднее квадратическое отклонение значения количества продаж продукта в день.
- Рассчитать общее среднее квадратическое отклонение.
- Рассчитать значение функции потерь $f(k)$.
- По рассчитанному значению функции потерь найти соответствующее значение коэффициента $k$.
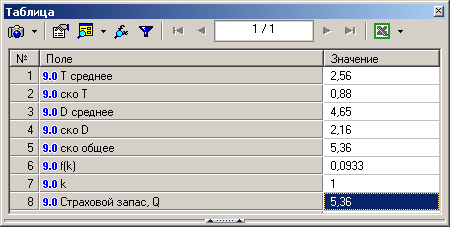
- Рассчитать значение страхового запаса для заданных значений величины дефицита и размера заказа.
Требования к данным
Календарь поставок
| Имя поля | Метка поля | Тип данных | Вид данных |
|---|---|---|---|
| Date_begin | Дата оформления заказа | Дата/время | Непрерывный |
| Date_end | Дата поставки | Дата/время | Непрерывный |
Продажи
| Имя поля | Метка поля | Тип данных | Вид данных |
|---|---|---|---|
| Date_sale | Дата продажи | Дата/время | Непрерывный |
| Count_sale | Объем продажи | Целый | Непрерывный |
Значения функции потерь f(k) и коэффициента k
| Имя поля | Метка поля | Тип данных | Вид данных |
|---|---|---|---|
| f_table | f(k) | Вещественный | Непрерывный |
| k | k | Вещественный | Непрерывный |
Сценарий