Social Mining: анализ информационных потоков в социальных сетях

Social Mining2 комментарияВерсия для печати

Введение

В крупных компаниях, активно использующих современные технологии обмена информацией, рано или поздно встает вопрос о контроле за этим обменом. Объемы переписки могут исчисляться сотнями, а то и тысячами сообщений в день. Злоумышленники могут без труда воспользоваться подобной ситуацией, чтобы вместе со служебной информацией распространять информацию конфиденциального характера. Формально подобное положение можно рассматривать как некоторую социальную сеть, объектами которой являются сотрудники фирмы, а количество сообщений, отправляемых одним человеком другому, – представить в виде дуг, имеющих соответствующие веса. После того как данные об обмене информацией реализованы в понятиях теории графов, мы получим граф подобный этому:

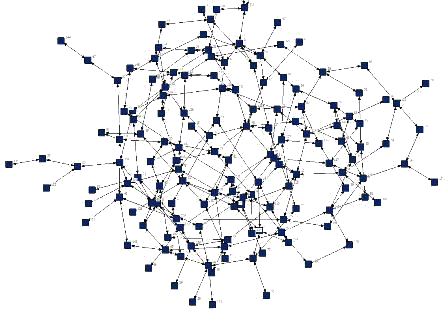
На рисунке изображена визуализация графа, имеющего порядка 150 вершин. Очевидно, что пытаться анализировать подобную схему визуально как минимум затруднительно, а учитывая, что количество объектов по большому счету неограниченно, подобные методы можно исключить сразу. Используя современные методы анализа информации и теории графов, можно перейти к более адекватным уровням анализа сетей.

Анализ

Естественно, что ограничиваться только машинным анализом связей не следует, с помощью него можно выявить только подозрительные узлы и наметить объекты, требующие более детального расследования. В качестве задач анализа можно выделить следующие:

• Поиск объектов, наиболее активно общающихся с представителями других фирм.
• Поиск объектов, наиболее активно участвующих в переписке внутри фирмы.
• Поиск объектов, имеющих наибольшее количество связей.
• Поиск наиболее "могущественных" объектов.
• Поиск объектов, имеющих наиболее активный входящий трафик сообщений и т.п.

Перейдем к рассмотрению примера. Разделим анализ на три этапа:

• Анализ связей объектов всей сети.
• Анализ связей на уровне фирм.
• Анализ связей объектов с фирмами.

Анализ связей объектов всей сети

Для получения наиболее корректной информации о месте объекта в сети необходимо проанализировать взаимодействия всех объектов, не разбивая их на группы и не исключая из рассмотрения ни одного из них, даже если на первый взгляд он кажется абсолютно не значимым.

Используя исходные данные о фактах связей, построим матрицу смежности графа. Матрицей смежности $A = [a_{ij}]$ графа $G$ называется квадратная матрица c размерностью $n*n$ (где $n$ – кол-во вершин), а элемент $a_{ij}$ определяется по следующему правилу:

$a_{ij} = 1$ – если в графе $G$ есть дуга $(x_i;x_j)$,

$a_{ij} = 0$ – если в графе $G$ отсутствует дуга $(x_i;x_j)$.

Далее, чтобы получить искомую информацию, построчно суммируем: $S_i=\sum \limits_{j=1}^{n}a_{ij}$.

Посчитав количество связей , мы можем сказать, какому числу объектов может быть передана информация. У нас есть возможность оценить степень влияния узлов сети, но каждый из них, на который оно оказывается, в свою очередь связан (или не связан) с другими узлами. Рассмотри более конкретный пример:

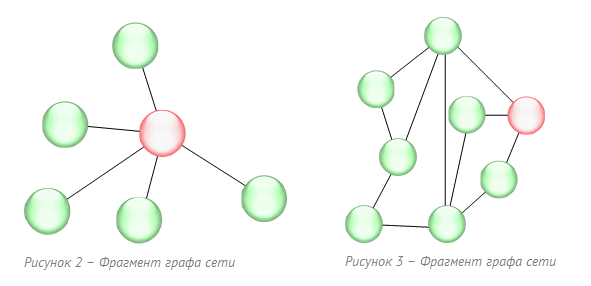
Объект на рисунке 2 обладает большим влиянием, но узлы, с которыми он связан, не имеют такого качества (никакого влияния). Объект на рисунке 3 имеет меньшее влияние, но он более могущественный, т.к. объекты, с которым он связан, также имеют некоторое влияние в сети.

Для поиска наиболее могущественного объекта сети (имеющего наибольшую силу) вычисляют итерированную силу порядка $k$ объекта $x_i (i=\overline{1,n}) $:

$p^i(k)=\sum \limits_{i=1}^{n}B*p^i(k-1)$

$p^i(0)=1$,

где $n$ – количество объектов сети, $B$ – матрица расстояний.

Матрица расстояний $В$ – это матрица вида

$B= \begin{pmatrix} b_{11} b_{12} \cdots b_{1n}\\ b_{21} b_{22} \cdots b_{2n}\\ \vdots\\ b_{n1} b_{n2} \cdots b_{nn} \end{pmatrix}$,

где $b_{ij}$ – количество связей между объектом $x_i$ и $x_j$.

Теперь введем понятие силы объекта, как предела при $k\rightarrow n$:

$P^i_k=\frac{p^{i}(k)}{\sum \limits_{i=1}^{n}p^{i}(k)}$.

Реализация

На вход алгоритма подаются данные вида: Номер объекта (N_1_i), Номер объекта (N_2_i), Количество связей (Count_i).

Шаг 1. Построение матрицы расстояний.

Шаг 2. Расчет итерированной силы 1-го порядка p(1) для каждого объекта:

Шаг 3. Расчет итерированной силы 2-го порядка p(2) для каждого объекта:

Шаг 4. Расчет итерированной силы 3-го порядка p(3) для каждого объекта:

Далее предыдущие шаги продолжаются для достижения необходимой точности. В идеале следует получить итерированную силу для всех объектов порядка $k – p(k)$, где $k$ стремится к n (количество объектов).

Шаг $(n-1)$. Расчет силы для каждого объекта в сети:

$P^i_k=\frac{p^{i}(k)}{\sum \limits_{i=1}^{n}p^{i}(k)}$.

Шаг $n$. Далее все объекты сортируются по значению рассчитанной силы $P$ и им присваивается значение рейтинга для объекта, у которого $Pmax$ – это $1$, и так далее по убыванию.

В результате получается подобная таблица.

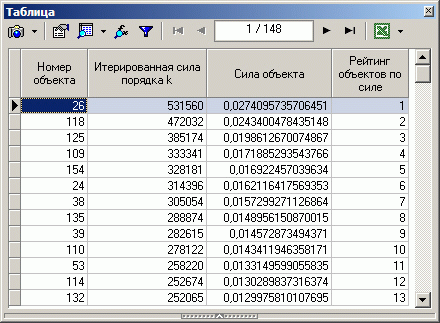
Используя информацию, полученную в результате этого алгоритма, можно делать выводы о том, какие объекты наиболее влиятельны в сети, какие способствуют наиболее эффективному распространению информации в ней (если, например, необходимо внутри этой сети распространить некую информацию, имея ограничение на кол-во обращений, то очевидно, что более эффективным будет начать распространение с объектов, расположенных в первых строках таблицы).

Анализ связей на уровне групп

Как правило, объекты сети можно объединить в группы по какому-то признаку: пол, фирма, отдел, город проживания и т.п. Тогда мы можем перейти на более высокий уровень анализа, например, если объектами сети являются работники разных фирм, которые каким-то образом связаны между собой, мы можем перейти от анализа связей объектов к анализу связей групп объектов (рисунок 5).

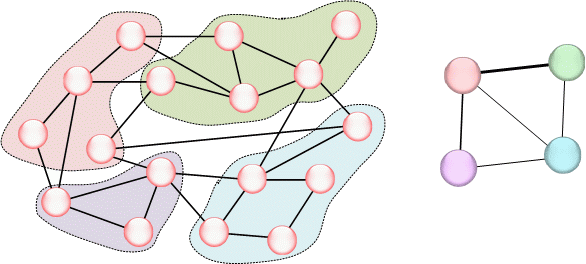
Далее с группами можно работать как с отдельными объектами, этот прием поможет, например, когда для удобства анализа надо сократить кол-во рассматриваемых объектов с нескольких тысяч до десятков.

Реализация

На вход алгоритма подадим информацию, аналогичную той, которая была представлена в предыдущем примере реализации, но дополним её сведениями о принадлежности объектов к группам: Номер объекта (N_1_i), Группа объекта N_1 (GN_1_i), Номер объекта (N_2_i), Группа объекта N_2 (GN_2_i), Количество связей (Count_i).

Шаг 1. Агрегация информации по группам.

Шаг 2. Расчет наибольшего количества исходящих сообщений для каждой группы.

Шаг 3. Расчет наибольшего количества входящих сообщений для каждой группы.

В результате получаются подобные таблицы:

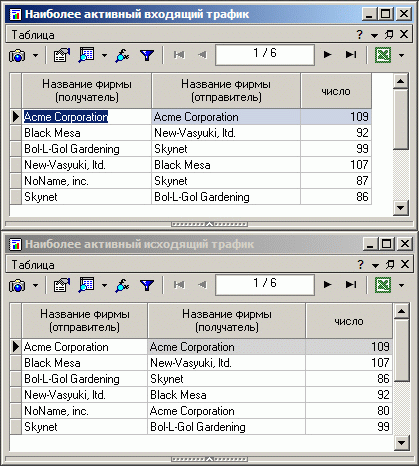
Используя таблицы, полученные в результате работы этого алгоритма, можно узнать, какие группы наиболее активно общаются, какие находятся в изоляции, кто является источником информации, а кто агрегирует ее.

Например, анализируя таблицы на рисунке 6, можно построить следующую картину:

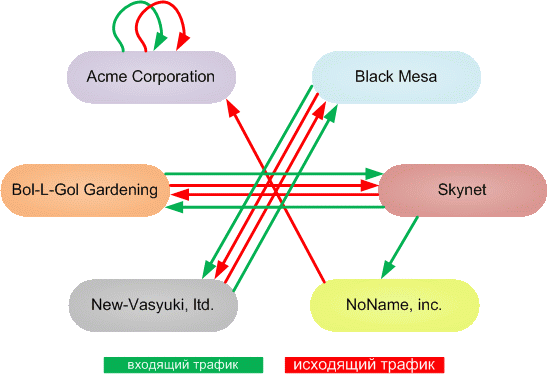
А глядя на эту схему (рисунок 7) можно сделать следующие выводы:

• Компании New-Vasyuki, ltd. и Black Mesa генерируют трафик между собой;
• Компании Bol-L-Gol Gardening и Skynet также генерируют трафик между собой;
• Компания NoName, inc. получает большее количество сообщений от Skynet и передает в компанию Acme Corporation;
• Компания Acme Corporation генерирует большую часть трафика внутри себя.

Из этого можно предположить, что группы компаний New-Vasyuki, ltd. + Black Mesa и Bol-L-Gol Gardening + Skynet две конкурирующие коалиции. Компания NoName, inc. является дочерней фирмой компании Acme Corporation.

Анализ связей объектов с группами

Для того чтобы работать с группами и наблюдать внутреннюю структуру связей между ними, необходимо анализировать связи объектов с группами.

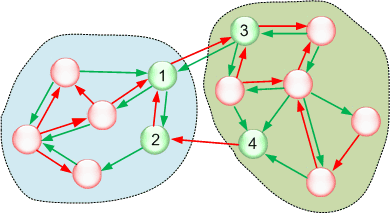
Рассмотрим ситуацию на рисунке 8. Группы связаны между собой через узлы 1-3 и 2-4. Причем связь 2-4 односторонняя (объект №4 передает сообщения объекту №2, не получая ответных сообщений), причем объект №4 имеет одностороннюю входящую связь внутри группы.

Реализация

Исходные данные те же, что и в предыдущем примере реализации: Номер объекта (N_1_i), Группа объекта N_1 (GN_1_i), Номер объекта (N_2_i), Группа объекта N_2 (GN_2_i), Количество связей (Count_i).

Шаг 1. Расчет наибольшего количества исходящих сообщений от объектов группы для каждой группы.

Шаг 2. Расчет наибольшего количества входящих сообщений для объектов группы от каждой группы.

Шаг 3. Формируются две таблицы : "Объекты, имеющие наибольшее число исходящих сообщений в другие группы" и "Объекты, имеющие наибольшее число входящих сообщений из других групп".

В результате работы алгоритма получаем подобные таблицы.

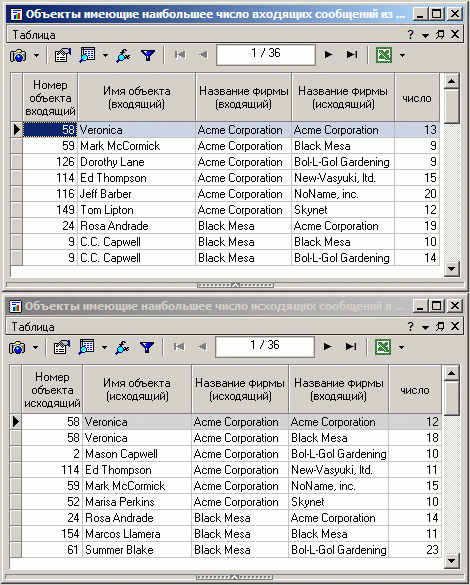
Проанализировав эту информацию можно сделать выводы о том, какие объекты являются связующими звеньями между группами, какие объекты сети генерируют наибольший трафик между группами.

Заключение

Используя анализ графов в социальных сетях, можно делать интересные и неочевидные выводы: какие объекты наиболее эффективны при распространении информации, какие объекты групп сети генерируют основной трафик между другими группами, какие группы объектов изолированы от сети и т.п. Эти выводы могут быть полезны в различных сферах:

• Интернет. Выявление лидеров мнений в социальных сетях, запуск "сарафанного радио", управление PR-акциями.
• Маркетинг. Анализ связей как одного из свойств клиентов для формирования более полного его "портрета", обогащение данных о клиенте.
• Реклама. Продвижение сложных товаров через сеть лояльных партнеров/клиентов, кросс-продажи.
• Безопасность. Поиск мест утечек конфиденциальной информации, выявление объектов источников дезинформации, обнаружение агентов влияния, мониторинг контактов между группами узлов сети.
• Корпоративная психология. Организация эффективных рабочих групп, формирование проектных команд.
• Оптимизация сети. Перераспределение мощностей для оптимальной обработки трафика.