Метод сопряженных градиентов — математический аппарат

Методология19 комментариевВерсия для печати

Термин "метод сопряженных градиентов" – один из примеров того, как бессмысленные словосочетания, став привычными, воспринимаются сами собой разумеющимися и не вызывают никакого недоумения. Дело в том, что, за исключением частного и не представляющего практического интереса случая, градиенты не являются сопряженными, а сопряженные направления не имеют ничего общего с градиентами. Название метода отражает тот факт, что данный метод отыскания безусловного экстремума сочетает в себе понятия градиента целевой функции и сопряженных направлений.

Несколько слов об обозначениях, используемых далее.

Скалярное произведение двух векторов записывается $x^Ty$ и представляет сумму скаляров: $\sum_{i=1}^n\, x_i\,y_i$. Заметим, что $x^Ty = y^Tx$. Если x и y ортогональны, то $x^Ty = 0$. В общем, выражения, которые преобразуются к матрице 1х1, такие как $x^Ty$ и $x^TA_x$, рассматриваются как скалярные величины.

Первоначально метод сопряженных градиентов был разработан для решения систем линейных алгебраических уравнений вида:

$A_x = b$, (1)

где x – неизвестный вектор, b – известный вектор, а A – известная, квадратная, симметричная, положительно–определенная матрица. Решение этой системы эквивалентно нахождению минимума соответствующей квадратичной формы.
Квадратичная форма – это просто скаляр, квадратичная функция некого вектора x следующего вида:

$f\,(x) = (\frac{1}{2})\,x^TA_x\,-\,b^Tx\,+\,c$, (2)

Наличие такой связи между матрицей линейного преобразования A и скалярной функцией f(x) дает возможность проиллюстрировать некоторые формулы линейной алгебры интуитивно понятными рисунками. Например, матрица А называется положительно-определенной, если для любого ненулевого вектора x справедливо следующее:

$x^TA_x\,>\,0$, (3)

На рисунке 1 изображено как выглядят квадратичные формы соответственно для положительно-определенной матрицы (а), отрицательно-определенной матрицы (b), положительно-неопределенной матрицы (с), неопределенной матрицы (d).

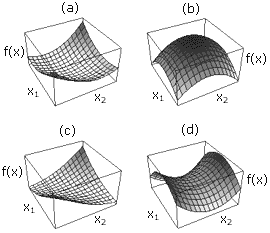
То есть, если матрица А – положительно-определенная, то вместо того, чтобы решать систему уравнений 1, можно найти минимум ее квадратичной функции. Причем, метод сопряженных градиентов сделает это за n или менее шагов, где n – размерность неизвестного вектора x. Так как любая гладкая функция в окрестностях точки своего минимума хорошо аппроксимируется квадратичной, этот же метод можно применить для минимизации и неквадратичных функций. При этом метод перестает быть конечным, а становится итеративным.

Рассмотрение метода сопряженных градиентов целесообразно начать с рассмотрения более простого метода поиска экстремума функции – метода наискорейшего спуска. На рисунке 2 изображена траектория движения в точку минимума методом наискорейшего спуска. Суть этого метода:

• в начальной точке x(0) вычисляется градиент, и движение осуществляется в направлении антиградиента до тех пор, пока уменьшается целевая функция;
• в точке, где функция перестает уменьшаться, опять вычисляется градиент, и спуск продолжается в новом направлении;
• процесс повторяется до достижения точки минимума.

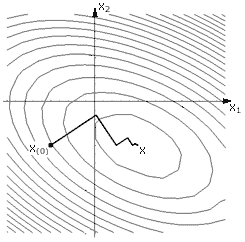
В данном случае каждое новое направление движения ортогонально предыдущему. Не существует ли более разумного способа выбора нового направления движения? Существует, и он называется метод сопряженных направлений. А метод сопряженных градиентов как раз относится к группе методов сопряженных направлений. На рисунке 3 изображена траектория движения в точку минимума при использовании метода сопряженных градиентов.

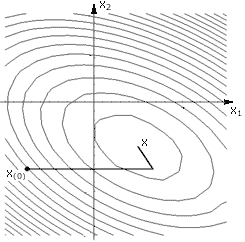
Определение сопряженности формулируется следующим образом: два вектора x и y называют А-сопряженными (или сопряженными по отношению к матрице А) или А–ортогональными, если скалярное произведение x и Ay равно нулю, то есть:

$x^TA_y\,=\,0$, (4)

Сопряженность можно считать обобщением понятия ортогональности. Действительно, когда матрица А – единичная матрица, в соответствии с равенством 4, векторы x и y – ортогональны. Можно и иначе продемонстрировать взаимосвязь понятий ортогональности и сопряженности: мысленно растяните рисунок 3 таким образом, чтобы линии равного уровня из эллипсов превратились в окружности, при этом сопряженные направления станут просто ортогональными.

Остается выяснить, каким образом вычислять сопряженные направления. Один из возможных способов – использовать методы линейной алгебры, в частности, процесс ортогонализации Грамма–Шмидта. Но для этого необходимо знать матрицу А, поэтому для большинства задач (например, обучение многослойных нейросетей) этот метод не годится. К счастью, существуют другие, итеративные способы вычисления сопряженного направления, самый известный – формула Флетчера-Ривса:

$d_{(i+1)} = d_{(i+1)}\,+\,\beta_{(i+1)}\,d_i$ , (5)

где:

$\beta_{(i+1)} = \frac{r_{(i+1)}^T}{r_{i}^T}\,\frac{r_{(i+1)}}{r_{(i)}}$, (6)

Формула 5 означает, что новое сопряженное направление получается сложением антиградиента в точке поворота и предыдущего направления движения, умноженного на коэффициент, вычисленный по формуле 6. Направления, вычисленные по формуле 5, оказываются сопряженными, если минимизируемая функция задана в форме 2. То есть для квадратичных функций метод сопряженных градиентов находит минимум за n шагов (n – размерность пространства поиска). Для функций общего вида алгоритм перестает быть конечным и становится итеративным. При этом, Флетчер и Ривс предлагают возобновлять алгоритмическую процедуру через каждые n + 1 шагов.

Можно привести еще одну формулу для определения сопряженного направления, формула Полака–Райбера (Polak-Ribiere):

$\beta_{(i+1)} = \frac{r_{(i+1)}^T\,(r_{(i+1)}\,-\,r_{(i)})}{r_{i}^T\,r_{(i)}}$, (7)

Метод Флетчера-Ривса сходится, если начальная точка достаточно близка к требуемому минимуму, тогда как метод Полака-Райбера может в редких случаях бесконечно циклиться . Однако последний часто сходится быстрее первого метода. К счастью, сходимость метода Полака-Райбера может быть гарантирована выбором $\beta = \max \{\beta;\,0\}$. Это эквивалентно рестарту алгорима по условию $\beta \leq 0$. Рестарт алгоритмической процедуры необходим, чтобы забыть последнее направление поиска и стартовать алгоритм заново в направлении скорейшего спуска.

Далее приведен алгоритм сопряженных градиентов для минимизации функций общего вида (неквадратичных).

1. Вычисляется антиградиент в произвольной точке x₍₀₎.
   

   $d_{(0)} = r_{(0)} = -\,f'(x_{(0)})$

2. Осуществляется спуск в вычисленном направлении пока функция уменьшается, иными словами, поиск a_(i), который минимизирует
   

   $f\,(x_{(i)}\,+\,a_{(i)}\,d_{(i)})$

3. Переход в точку, найденную в предыдущем пункте
   

   $x_{(i+1)} = x_{(i)}\,+\,a_{(i)}\,d_{(i)}$

4. Вычисление антиградиента в этой точке
   

   $r_{(i+1)} = -\,f'(x_{(i+1)})$

5. Вычисления по формуле 6 или 7. Чтобы осуществить рестарт алгоритма, то есть забыть последнее направление поиска и стартовать алгоритм заново в направлении скорейшего спуска, для формулы Флетчера–Ривса присваивается 0 через каждые n + 1 шагов, для формулы Полака-Райбера – $\beta_{(i+1)} = \max \{\beta_{(i+1)},\,0\}$
   
6. Вычисление нового сопряженного направления
   

   $d_{(i+1)} = r_{(i+1)}\,+\,\beta_{(i+1)}\,d_{(i)}$

7. Переход на пункт 2.

Из приведенного алгоритма следует, что на шаге 2 осуществляется одномерная минимизация функции. Для этого, в частности, можно воспользоваться методом Фибоначчи, методом золотого сечения или методом бисекций. Более быструю сходимость обеспечивает метод Ньютона–Рафсона, но для этого необходимо иметь возможность вычисления матрицы Гессе. В последнем случае, переменная, по которой осуществляется оптимизация, вычисляется на каждом шаге итерации по формуле:

$$a = -\,\frac{{f'}^T\,(x)\,d}{d^T\,f''(x)\,d}$$

где

$f''(x)\,= \begin{pmatrix} \frac{\partial^2\,f}{\partial x_1\,\partial x_1}&\frac{\partial^2\,f}{\partial x_1\,\partial x_2}&\cdots&\frac{\partial^2\,f}{\partial x_1\,\partial x_n}& \\ \frac{\partial^2\,f}{\partial x_2\,\partial x_1}&\frac{\partial^2\,f}{\partial x_2\,\partial x_2}& \cdots&\frac{\partial^2\,f}{\partial x_2\,\partial x_n}& \\ \vdots&\vdots&\ddots&\vdots &\\ \frac{\partial^2\,f}{\partial x_n\,\partial x_1}& \frac{\partial^2\,f}{\partial x_n\,\partial x_2}&\cdots&\frac{\partial^2\,f}{\partial x_n\,\partial x_n} \end{pmatrix}$
Матрица Гессе

Это дает основания некоторым авторам относить метод сопряженных градиентов к методам второго порядка, хотя суть метода вовсе не предполагает необходимым вычисление вторых производных.

Несколько слов об использовании метода сопряженных направлений при обучении нейронных сетей. В этом случае используется обучение по эпохам, то есть при вычислении целевой функции предъявляются все шаблоны обучающего множества и вычисляется средний квадрат функции ошибки (или некая ее модификация). То же самое – при вычислении градиента, то есть используется суммарный градиент по всему обучающему набору. Градиент для каждого примера вычисляется с использованием алгоритма обратного распространения (BackProp).

В заключение приведем один из возможных алгоритмов программной реализации метода сопряженных градиентов. Сопряженность в данном случае вычисляется по формуле Флетчера–Ривса, а для одномерной оптимизации используется один из вышеперечисленных методов. По мнению некоторых авторитетных специалистов скорость сходимости алгоритма мало зависит от оптимизационной формулы, применяемой на шаге 2 приведенного выше алгоритма, поэтому можно рекомендовать, например, метод золотого сечения, который не требует вычисления производных.

Вариант метода сопряженных направлений, использующий формулу Флетчера-Ривса для расчета сопряженных направлений.

Метод сопряженных градиентов является методом первого порядка, в то же время скорость его сходимости квадратична. Этим он выгодно отличается от обычных градиентных методов. Например, метод наискорейшего спуска и метод координатного спуска для квадратичной функции сходятся лишь в пределе, в то время как метод сопряженных градиентов оптимизирует квадратичную функцию за конечное число итераций. При оптимизации функций общего вида, метод сопряженных направлений сходится в 4-5 раз быстрее метода наискорейшего спуска. При этом, в отличие от методов второго порядка, не требуется трудоемких вычислений вторых частных производных.