Введение
Дерево решений – широко известный и популярный метод автоматического анализа данных, в основе которого лежит обучение на примерах. Правила представлены в виде иерархической последовательной структуры, где каждый объект принадлежит конкретному узлу.
Однако может возникнуть случай, когда точно классифицировать объект по тому или иному признаку довольно трудно. Эти ситуации разрешаются благодаря возможностям нечеткой логики, когда говорят не просто о принадлежности к кому-то классу, признаку, атрибуту, а о её степени. При использовании нечетких деревьев решений (fuzzy decision trees) не теряются знания о том, что объект может обладать свойствами как одного признака, так и другого в той или иной мере.
Главной идеей в таком подходе является сочетание возможностей деревьев решений и нечеткой логики.
Алгоритм построения нечеткого дерева решений
Отличительной чертой деревьев решений является то, что каждый пример определенно принадлежит конкретному узлу. В нечетком случае это не так. Для каждого атрибута необходимо выделить несколько его лингвистических значений и определить степени принадлежности примеров к ним. Вместо количества примеров конкретного узла нечеткое дерево решений группирует их степень принадлежности. Коэффициент – это соотношение примеров $D_j\,\in\,S^N$ узла $N$ для целевого значения $i$, вычисляемый как:
$P_i^N = \sum_{S^N} \,\min\,(\mu_N\,(D_j),\,\mu_i\,(D_j))$, (1)
где $mu_N\,(D_j)$ – степень принадлежности примера $D_j$ к узлу $N$, $mu_i\,(D_j)$ – степень принадлежности примера относительно целевого значения $i$, $S^N$ – множество всех примеров узла $N$. Затем находим коэффициент $P^N$, обозначающий общие характеристики примеров узла $N$. В стандартном алгоритме дерева решений определяется отношение числа примеров, принадлежащих конкретному атрибуту, к общему числу примеров. Для нечетких деревьев используется отношение $\frac{P_i^N}{P^N}$, для расчета которого учитывается степень принадлежности.
Выражение
$E\,(S^N) = -\,\sum_i \frac{P_i^N}{P^N}\,\cdot\,\log_2 \frac{P_i^N}{P^N}$, (2)
даёт оценку среднего количества информации для определения класса объекта из множества $P^N$.
На следующем шаге построения нечеткого дерева решений алгоритм вычисляет энтропию для разбиения по атрибуту $A$ со значениями $a_j$:
$E\,(S^N,\,A) = \sum_j \frac{P^{N\mid j}}{P^N}\,\cdot\,E\,(S^{N\mid j})$, (3)
где узел $N\mid j$ – дочерний для узла $N$.
Алгоритм выбирает атрибут $A^{\times}$ с максимальным приростом информации:
$G\,(S^N,\,A) = E\,(S^N)\,-\,E\,(S^N,\,A)$, (4)
$A^{\times} = argmax_A\,G\,(S,\,A)$, (5)
Узел $N$ разбивается на несколько подузлов $N\mid j$. Степень принадлежности примера $D_k$ узла $N\mid j$ вычисляется пошагово из узла $N$ как
$\mu_{N\mid j}\,(e_k) = \min\,(\mu_{N\mid j}\,(D_k),\,\mu_{N\mid j}\,(D_k,\,a_j))$, (6)
где $\mu_{N\mid j}\,(D_k,\,a_j))$ показывает степень принадлежности $D_k$ к атрибуту $a_j$.
Подузел $N\mid j$ удаляется, если все примеры в нем имеют степень принадлежности, равную нулю. Алгоритм повторяется до тех пор, пока все примеры узла не будут классифицированы либо пока не будут использованы для разбиения все атрибуты.
Принадлежность к целевому классу для новой записи находится по формуле
$\sigma_j = \frac{\sum_l \sum_k P_k^l\,\cdot\,\mu_l\,(D_j)\,\cdot\,\chi_k}{\sum_l \,(\mu_l\,(D_j)\,\cdot\,\sum_k P_k^l)}$, (7)
где
$P_k^l$ – коэффициент соотношения примеров листа дерева $l$ для значения целевого класса $k$,
$\mu_l\,(D_j)$ – степень принадлежности примера к узлу $l$,
$\chi_k$ – принадлежность значения целевого класса $k$ к положительному значению исхода классификации.
Пример
В таблице 1 представлены данные о семи клиентах банка: проживание в регионе (в годах), доход (в денежных единицах) и рейтинг выдачи ему кредита. Необходимо построить нечеткое дерево решений, с помощью которого определить рейтинг выдачи кредита для клиента, который проживает в регионе 25 лет, и доход его составляет 32 000 (будет решаться задача регрессии).
Таблица 1 – Обучающие примеры для построения нечеткого дерева решений
| № | Проживание в регионе | Доход | Рейтинг |
|---|---|---|---|
| D1 | 0 |
10 000 |
0,0 |
| D2 | 10 |
15 000 |
0,0 |
| D3 | 15 |
20 000 |
0,1 |
| D4 | 20 |
30 000 |
0,3 |
| D5 | 30 |
25 000 |
0,7 |
| D6 | 40 |
35 000 |
0,9 |
| D7 | 40 |
50 000 |
1,0 |
Предположим, что атрибут "проживание в регионе" может принимать значения "временно", "продолжительно", "постоянно", а атрибут "доход" – "малый", "средний" и "высокий". Степень принадлежности каждого примера к значениям атрибутов представлена в таблице 2. Общий вид функции для атрибутов показан на рисунке 1.
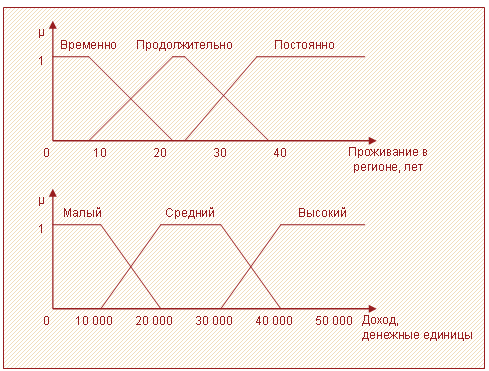
Таблица 2 – Степень принадлежности примеров к атрибутам
| № | Проживание в регионе | Доход | ||||
|---|---|---|---|---|---|---|
| Временно | Продолжительно | Постоянно | Малый | Средний | Высокий | |
| D1 | 1 |
0 |
0 |
1 |
0 |
0 |
| D2 | 0,8 |
0,2 |
0 |
0,6 |
0,4 |
0 |
| D3 | 0,5 |
0,5 |
0 |
0,1 |
0,9 |
0 |
| D4 | 0,2 |
0,8 |
0 |
0 |
1 |
0 |
| D5 | 0 |
0,5 |
0,5 |
0 |
1 |
0 |
| D6 | 0 |
0 |
1 |
0 |
0,6 |
0,4 |
| D7 | 0 |
0 |
1 |
0 |
0 |
1 |
В начале необходимо найти значение – общая энтропия.
Pда = 0 + 0 + 0,1 + 0,3 + 0,7 + 0,9 + 1,0 = 3,
Pнет = 1 + 1 + 0,9 + 0,7 + 0,3 + 0,1 + 0 = 4,
P = Pда + Pнет = 3 + 4 = 7,
$E\,(S^N) = -\,\frac{3}{7}\,\cdot\,\log_2 \frac{3}{7}\,-\,\frac{4}{7}\,\cdot\,\log_2 \frac{4}{7}\,\approx\,0,985$ бит.
Теперь рассчитаем $\;E\,(S^N,$ проживание в регионе).
Pдавременно = min(0;1) + min(0;0,8) + min(0,1;0,5) + min (0,3;0,2) + min(0,7;0) + min(0,9;0) + min(1;0) = 0 + 0 + 0,1 + 0,2 + 0 + 0 + 0 = 0,3
Pнетвременно = min(1;1) + min(1;0,8) + min(0,9;0,5) + min (0,7;0,2) + min(0,3;0) + min(0,1;0) + min(0;0) = 1 + 0,8 + 0,5 + 0,2 + 0 + 0 + 0 = 2,5
Pвременно = 0,3 + 2,5 = 2,8
E(проживание в регионе, временно)= $\;-\,\frac{0,3}{2,8}\,\cdot\,\log_2 \frac{0,3}{2,8}\,-\,\frac{2,5}{2,8}\,\cdot\,\log_2 \frac{2,5}{2,8}\,\approx\,0,491$ бит.
Для продолжительного и постоянного проживания в регионе проводятся аналогичные вычисления. Результат сведем в таблицу 3.
Таблица 3 – Итог расчетов для атрибута "проживание в регионе"
| Временно | Продолжительно | Постоянно | |
|---|---|---|---|
| Pда | 0,3 |
0,9 |
2,4 |
| Pнет | 2,5 |
1,7 |
0,4 |
| E в битах | 0,491 |
0,931 |
0,592 |
Отсюда находим энтропию:
E(SN, проживание в регионе)= $\frac{2,5}{7}\,\cdot\,0,491\,+\,\frac{2}{7}\,\cdot\,0,931\,+\,\frac{2,5}{7}\,\cdot\,0,592\,=\,0,653$ бит.
Рассчитаем прирост информации для данного атрибута.
G(SN, проживание в регионе) = 0,985 - 0,653 = 0,332 бит.
Проводя подобные вычисления для атрибута "доход", получаем
E(SN, доход) = 0,691 бит,
G(SN, доход) = 0,294 бит.
Максимальный прирост информации обеспечивает атрибут "проживание в регионе", следовательно, разбиение начнется с него.
На следующем шаге алгоритма необходимо для каждой записи рассчитать степень принадлежности к каждому новому узлу по формуле (6). Результат представлен в таблице 4.
Таблица 4 – Принадлежность записей новым узлам дерева
| Проживание в регионе | временно | продолжительно | постоянно | ||||||
|---|---|---|---|---|---|---|---|---|---|
| доход | малый | средний | высокий | малый | средний | высокий | малый | средний | высокий |
| D1 | 1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| D2 | 0,6 |
0,4 |
0 |
0,2 |
0,2 |
0 |
0 |
0 |
0 |
| D3 | 0,1 |
0,5 |
0 |
0,1 |
0,5 |
0 |
0 |
0 |
0 |
| D4 | 0 |
0,2 |
0 |
0 |
0,8 |
0 |
0 |
0 |
0 |
| D5 | 0 |
0 |
0 |
0 |
0,5 |
0 |
0 |
0,5 |
0 |
| D6 | 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,6 |
0,4 |
| D7 | 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
К узлам [проживание в регионе = временно и доход = высокий] и [проживание в регионе = продолжительно и доход = высокий] не принадлежит ни одна запись, поэтому они удаляются из дерева.
Для каждого узла находятся коэффициенты $P_i^N$. Полученное дерево представлено на рисунке 2.
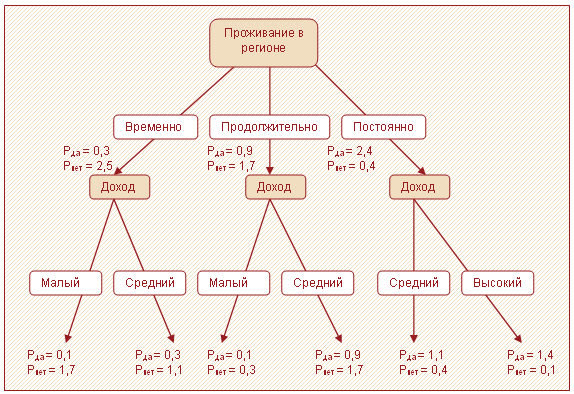
Теперь определим кредитный рейтинг для клиента, проживающего в регионе 25 лет, и с доходом 30 000.
За положительный исход в данной задаче принято одобрение в выдаче кредита, поэтому χ да = 1,0, χнет = 0,0. Новый клиент принадлежит к двум узлам: [проживание в регионе = продолжительно и доход = средний] и [проживание в регионе = постоянно и доход = средний], со степенями 0,8 и 0,2 соответственно. Подставляя полученные значения в формулу (7), рассчитываем кредитный рейтинг:
$$ \delta = \frac{0,9\,\times\,0,8\,\times\,1,0\,+\,1,7\,\times\,0,8\,\times\,0,0\,+\,1,1\,\times\,0,8\,\times\,1,0\,+\,0,4\,\times\,0,2\,\times\,0,0}{(0,9\,+\,1,7)\,\times\,0,8\,+\,(1,1\,+0,4)\,\times\,0,2} = 0,395$$
В итоге мы получили кредитный рейтинг, равный 0,395. Он означает, что степень принадлежности записи к тому, что кредит клиенту будет выдан, равна 0,395, а к невыдаче – 0,605. Следовательно, этому клиенту банком будет отказано.
Решая задачу классификации, выбирается тот класс $i$, для которого значение $P_i$ максимально.
Применение и основные выводы
Нечеткие деревья решений применяются в Data Mining как для решения задач классификации, так и для решения задачи регрессии, когда необходимо знать степени принадлежности к тому или иному исходу. Они могут быть использованы в различных областях: в банковском деле для решения задачи скоринга, в медицине для диагностики различных заболеваний, в промышленности для контроля качества продукции и так далее.
Безусловным достоинством данного подхода является высокая точность классификации, достигаемая за счет сочетания достоинств нечеткой логики и деревьев решений. Процесс обучения происходит быстро, а результат прост для интерпретации. Так как алгоритм способен выдавать для нового объекта не только класс, но и степень принадлежности к нему, это позволяет управлять порогом для классификации.
Однако для этого необходим репрезентативный набор обучающих примеров, в противном случае сгенерированное алгоритмом дерево решений будет слабо отражать действительность и, как следствие, выдавать ошибочные результаты.
- Cordon O., Herrera F., Hoffmann F., Magdalena L. “Genetic fuzzy systems. Evolutionary tuning and learning of fuzzy knowledge bases”, 2001.
- Janikow C.Z. “Fuzzy Decision Trees: Issues and Methods”, 1996.
- Wang J. “Encyclopedia of data warehousing and mining”, 2006.
